本節では,ロジスティック回帰係数を確率に変換する方法について述べる。 また,係数の解釈のしかたを,対数オッズ,オッズ,オッズ比の観点から 述べる。二値変数・順序変数・名義変数のロジスティック回帰の扱いについては Agresti(1996, 2002), Hosmer&Lemeshow(2000)を参照のこと。
オッズとは2つの確率の比である。従って,対数オッズとは 2つの確率の比の対数である。対数オッズの指数はオッズである。 ロジスティック回帰係数は対数オッズである(ロジットともいう)。
二値従属変数 u についてのロジスティック回帰モデルを考えよう。 x の下での u の確率は下式で表現される:
P(u=1 | x) = exp(a + b*x) / (1+exp(a + b*x)) = 1 / (1+exp(-a - b*x))
ここから下式の線形ロジスティック回帰表現が得られる:
log [ P(u=1 | x) / P(u=0 | x) ] = log [exp(a + b*x)] = a + b*x
bはロジスティック回帰係数で,xが1単位増大したとき,u=1 と u=0 の対数オッズが どれだけ増大するかをあらわしている。たとえば,xの値として x_0 と x_0 + 1を 考えよう。対応する対数オッズは,
log odds (x_0) = a + b*x_0, log odds (x_0+1) = a + b*(x_0+1) = a + b*(x_0) + b,
xがx_0からx_0+1に増えたことで,対数オッズがbだけ増えている。つまり,オッズは exp(b) だけ増える。たとえば,抑うつの有無を従属変数とするロジスティック回帰モデルで連続的共変量として年齢が用いられており,その係数が0.75であるとしよう。このことは,年齢が1歳あがると,抑うつのあり対なしの対数オッズが0.75だけ増えるということを意味している。つまり,オッズは2.12増える。
x が二値の共変量(値は0,1)であるとき,u=1 と u=0 の対数オッズは
log odds (x=0) = a + b*0, log odds (x=1) = a + b*1,
だから,対数オッズは b だけ増える。log(y) - log(x) = log(y/z)だから, 二つの対数オッズの差
b = log odds(x=1) - log odds (x=0) = log[ odds(x=1)/odds(x=0) ]
は,x=1のときとx=0のときを比べた,u=1とu=0の対数オッズ比である。 たとえば,抑うつの有無を従属変数とするロジスティック回帰モデルで二値共変量として性別が用いられており(1=女性, 0=男性),その係数が1.0であるとしよう。このことは,抑うつのあり対なしの対数オッズが,男性より女性において1.0だけ大きいということを意味している。つまり,オッズは2.72倍大きい。
二値従属変数の場合は,最初のカテゴリ u=0 を参照カテゴリにする慣習がある。 従属変数のカテゴリ数が2より大きかった場合は, 最後のカテゴリを参照カテゴリにする慣習がある。 3カテゴリの名義変数の場合は,以下の多項ロジスティック回帰に 一般化できる。カテゴリ数をRとして,
P(u=r | x) = exp(a_r + b_r*x) / (分子のR個の合計)
ここで exp(a_R + b_R*x) = exp(0 + 0*x) = 1である。 カテゴリRに対するカテゴリrの対数オッズは
log [ P(u=r | x) / P(u=R | x) ] = a_r + b_r*x
順序変数の場合は,傾き b_r がuのどのカテゴリでも等しくなる。
モデルにおけるカテゴリカル潜在変数が名義従属変数である 場合について考える。 このカテゴリカル潜在変数は4クラスを持っており,共変量が3つある。 以下の出力は,カテゴリカル潜在変数c,共変量age94, male, blackの 多項ロジスティック回帰の結果である。
Estimates
C#1 ON
age94 -.285
male 2.578
black .158
C#2 ON
age94 .069
male .187
black -.606
C#3 ON
age94 -.317
male 1.459
black .999
Intercepts
C#1 -1.822
C#2 -.748
C#3 -.324
ある特定のクラスを最後のクラスと比べた対数オッズは,
log odds = a + b_1*age94 + b_2*male + b3*black
3つの共変量がすべて0である場合について考えよう。 まず,切片の対数オッズを指数にして合計する。 次に,指数を合計で割る。これが,cのそれぞれのクラスの確率になる。
exp prob=exp/sum
log odds (c=1) = -1.822 0.162 0.069
log odds (c=2) = -0.748 0.473 0.201
log odds (c=3) = -0.324 0.723 0.307
log odds (c=4) = 0 1.0 0.474
sum 2.358 1.001
3つの共変量がすべて1である場合について考えよう。 まず,各クラスの対数オッズを求める。 次に,それを指数にする。最後に,指数を合計で割る。 これがcのそれぞれのクラスの確率になる。
log odds (c=1) = -1.822+(-0.285*1)+(2.578*1)+(0.158*1) = 0.629 log odds (c=2) = -0.748 + 0.069*1 + 0.187*1 + (-0.606*1) = -1.098 log odds (c=3) = -0.324 + (-0.317*1) + 1.459*1 + 0.999*1 = 1.817
exp prob=exp/sum
log odds (c=1) = 0.629 1.876 0.200
log odds (c=2) = -1.098 0.334 0.036
log odds (c=3) = 1.817 6.153 0.657
log odds (c=4) = 0 1.0 0.107
sum 9.363 1.000
これらの確率は次のように解釈できる。ある人がそれぞれの共変量について値 1 を持っているとき、その人がクラス 1 に属する確率は 0.200, クラス 2 に属する確率は 0.036, クラス 3 に属する確率は 0.657, クラス 4 に属する確率は 0.107 である。
上で示した出力では、変数 male は男性は値1, 女性は値0を持つ変数であり、 変数 blackは黒人は値1, 非黒人は値0を持つ変数であり、変数 age94 は16歳は値0, 17歳は値1, ..., 23歳は値7を持つ変数である。クラス1についてのロジスティック回帰 係数を解釈するひとつのやりかたは、クラス1を4と比べることである。 対数オッズは、年齢が1単位上昇すると-0.285減少し、女性よりも男性において2.578高く、非黒人よりも黒人において0.158高い。このことは、(クラス4に対して)クラス1に属するオッズ比が、他の2つの共変量が一定ならば、女性に対して男性で13.17 (=exp(2.578))高いということを示している。
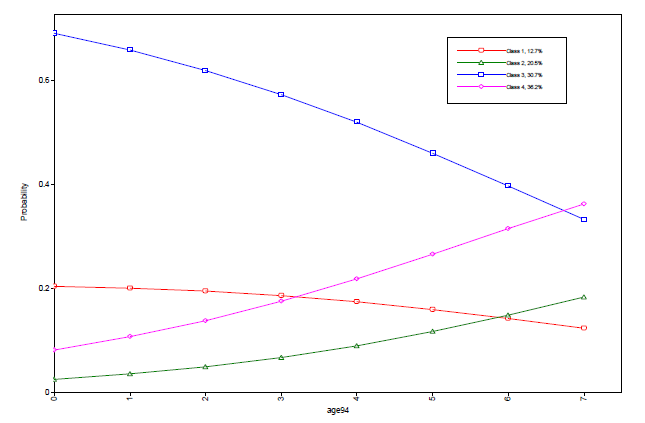
以下に示すのは、他の共変量の値を1としてに、年齢をx軸にとり、4つのクラスのそれぞれの推定確率をプロットしたものである。このプロットは、Mplus postprocessing graphicsモジュールとPLOTコマンドを併用し、EMFファイルとして生成・出力したものである。