選択型コンジョイント分析の実験計画をRでつくる

1 これはなに？

アンケート調査かなにかのなかで選択型コンジョイント分析をやりたいとき、 実験計画に十分気を配る必要がある。ひとり何試行を行うか？ 各試行ではどんな刺激を提示するのか？ 提示する刺激は、調査対象者によって共通にするか、それとも変動させるか？ どういう刺激をどういう順序で提示するのか？ 決めなければならないことがたくさんある。こういう点をないがしろにすると、後々困ったことになる。

世の中には実験計画についての解説が溢れている。ところが選択型コンジョイント分析の実験計画については解説が意外に少ない。広く普及している手法なのに、なぜだろう？ そのひとつの理由は、選択型コンジョイント分析の実験計画作成からデータ収集・解析までを一貫して行うシステムが市販されているためだろう (Sawtooth Software社のLighthouse Studioが有名である)。最近では選択型コンジョイント分析を組み込んだWeb調査を手軽に行えるDIY型サービスもある(conjointlyとか)。黙っていてもソフトがイイカンジの実験計画を作ってくれるわけだ。現代の調査者にとって、選択型コンジョイント分析のための実験計画の作成方法は必須知識とはいいがたい。

本文書は選択型コンジョイント分析の実験計画をRでつくる方法についてまとめたものだが、自力でそんなことを試みる前に、なにか別の方法や生き方を探した方が良いと思う。市販ソフトを買うとか、DIY型Webサービスを使うとか、専門の業者さんに相談するとか、部下に押しつけるとか、選択型コンジョイント分析をやめるとか、別の仕事を探すとか。

以下では、選択型コンジョイント分析の実験計画作成のうち、その基本的なスペック(属性と水準、調査対象者数、試行数、選択肢数など)が決まった後、それに基づき実験計画を生成する段階に注目する。基本的スペックの設定については触れない。データ収集・分析についても扱わない。

本文書は本質的に私による私のための私のメモなので、親切さは期待しないでほしい。日本語で読める親切な解説としては合崎・西村(2007)、合崎(2015)があるが、最適計画については扱っていない。最適計画についてのわかりやすい解説があったらぜひ読みたいんだけど… 本文書での説明は、idefixパッケージの作者らによる解説 (Traets, Sanchez, Vandebroek, 2020)を参考にしている。

選択型コンジョイント分析そのものについての解説はピンからキリまで山のようにあり、どちらかというとキリが多い。特にその辺のブログとかは要注意である(本文書とかね)。市場調査の文脈での解説としては、朝野(2012)とかチャップマン & フェイト(2020)とかがよいと思う。もし英語でよければ、そして調査実務家の方ならば、Sawtooth Software社によるOrme(2009), Orme & Chrzan(2021)の二冊が断然おすすめである。

2 Rパッケージ

実験計画作成のためのRパッケージはたくさんある。CRAN Task Viewの”Design of Experiments (DoE) & Analysis of Experimental Data”(Groemping & Mogan-Wall, 2023)で概観できる 。しかし、たいていのパッケージは実験計画法についてのかなりの知識を必要とする。

選択型コンジョイント分析の実験計画を簡単に作れるパッケージは、従来なかなか見当たらなかった。強いて言えばchoiceDes, support.CEs, idefixあたりが選択肢だったと思う。ところが最近になって cbcTools が出現した。これがとても使いやすい。選択型コンジョイント分析ユーザの今後のスタンダードになるのではないか(←「俺これからはこれを使おうかな」の荘重な表現)。

いっぽう、cbcToolsはあまりにユーザフレンドリーであり、中でなにをやっているのか、いささか不安になる。本文書はcbcToolsパッケージのソースコードを眺め、その中味を探った記録である。

使用する環境とパッケージは以下の通り。cbcToolsパッケージは現時点(2023/08/10)での最新版である0.5.1を使っている。CRAN公開版の0.5.0にはバグがあるのでご注意を。

library(cbcTools)
library(dplyr)
options(dplyr.summarise.inform = FALSE)
library(tidyr)
library(makedummies)
library(AlgDesign)
library(idefix)
library(mlogit)
library(GGally)

sessionInfo() 

R version 4.3.1 (2023-06-16 ucrt)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 19045)

Matrix products: default


locale:
[1] LC_COLLATE=Japanese_Japan.utf8  LC_CTYPE=Japanese_Japan.utf8   
[3] LC_MONETARY=Japanese_Japan.utf8 LC_NUMERIC=C                   
[5] LC_TIME=Japanese_Japan.utf8    

time zone: Asia/Tokyo
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] GGally_2.1.2      ggplot2_3.4.2     mlogit_1.1-1      dfidx_0.0-5      
 [5] idefix_1.0.3      shiny_1.7.4.1     AlgDesign_1.2.1   makedummies_1.2.1
 [9] tidyr_1.3.0       dplyr_1.1.2       cbcTools_0.5.1   

loaded via a namespace (and not attached):
 [1] utf8_1.2.3         generics_0.1.3     lattice_0.21-8     digest_0.6.33     
 [5] magrittr_2.0.3     RColorBrewer_1.1-3 evaluate_0.21      grid_4.3.1        
 [9] fastmap_1.1.1      plyr_1.8.8         jsonlite_1.8.7     reshape_0.8.9     
[13] Formula_1.2-5      promises_1.2.0.1   purrr_1.0.1        fansi_1.0.4       
[17] scales_1.2.1       Rdpack_2.4         cli_3.6.1          rlang_1.1.1       
[21] rbibutils_2.2.13   ellipsis_0.3.2     munsell_0.5.0      withr_2.5.0       
[25] yaml_2.3.7         tools_4.3.1        colorspace_2.1-0   httpuv_1.6.11     
[29] vctrs_0.6.3        R6_2.5.1           mime_0.12          zoo_1.8-12        
[33] lifecycle_1.0.3    htmlwidgets_1.6.2  MASS_7.3-60        pkgconfig_2.0.3   
[37] pillar_1.9.0       later_1.3.1        gtable_0.3.3       glue_1.6.2        
[41] Rcpp_1.0.11        statmod_1.5.0      xfun_0.39          tibble_3.2.1      
[45] lmtest_0.9-40      tidyselect_1.2.0   rstudioapi_0.15.0  knitr_1.43        
[49] xtable_1.8-4       htmltools_0.5.5    rmarkdown_2.23     compiler_4.3.1    

3 実験計画のつくりかた

cbcToolsパッケージの使用説明書 にある例題を使って説明しよう。リンゴについての選択型コンジョイント分析である。調査対象者に提示する刺激 (以下ではプロファイルと呼ぶ) は次の3つの属性の束である。

• 1パウンドあたり価格。{1, 1.5, …, 5}の9水準。
• 品種。{“Fuji”, “Gala”, “Honeycrisp”}の3水準。
• 品質。{“Poor”, “Average”, “Excellent”}の3水準。

よって、提示しうるプロファイルは 9x3x3=81 個ある。

以下の方針をとることにしよう。

• 81個のプロファイルを全て使用する。つまり、いわゆるprohibitionは行わない。
• データ収集にあたっては、「どれも選ばない」という選択肢も提示することにする。つまり、「どれも選ばない」という82番目のプロファイルが存在するわけである。上記の3属性のほかに「どれも選ばない」という二値属性があり、81個のプロファイルについては値は0、「どれも選ばない」プロファイルのみ値が1だ、と捉えることができる。
• 属性「1パウンドあたり価格」は連続的属性とみなす。つまり、9水準それぞれの部分効用を推定するのではなく、1パウンドあたり価格と部分効用のあいだに線形な関係があると仮定して、1単位あたりの部分効用を推定する。
• 交互作用項の推定は行わない。

推定すべきパラメータの数は、1(1パウンドあたり価格) + 2(品種) + 2(新鮮さ) + 1(どれも選ばない) = 6 となる。

では、cbcToolsパッケージで実験計画をつくってみよう。びっくりするくらい簡単である。

まず、81個のプロファイルを列挙したデータフレームをつくる。

profiles <- cbc_profiles(
  price     = seq(1, 5, 0.5), 
  type      = c('Fuji', 'Gala', 'Honeycrisp'),
  freshness = c('Poor', 'Average', 'Excellent')
)
head(profiles)

  profileID price type freshness
1         1   1.0 Fuji      Poor
2         2   1.5 Fuji      Poor
3         3   2.0 Fuji      Poor
4         4   2.5 Fuji      Poor
5         5   3.0 Fuji      Poor
6         6   3.5 Fuji      Poor

cbcToolsのドキュメントに説明が見当たらないが、どうやら水準を数値ベクトルとして指定した属性 (この例ではprice) は、あとで連続的属性として扱われるようだ。

次に、実験計画をつくる。以下ではある調査対象者に提示されるひとつの選択型設問を「試行」、そこで提示されるいくつかのプロファイルのそれぞれを「選択肢」と呼ぶことにしよう。

set.seed(123)
design <- cbc_design(
  profiles = profiles,
  n_resp   = 100,     # 調査対象者数
  n_alts   = 3,       # 試行あたり選択肢数。ただし「どれも選ばない」は除く
  n_q      = 6,       # 調査対象者あたり試行数
  no_choice = TRUE,   # 「どれも選ばない」を含める
  method   = 'random' # 実験計画の生成方法。後述する
)

method 引数で実験計画の生成方法を指定する。6種類の生成方法(random, full, orthogonal, dopt, CED, Modfed)が用意されている。それぞれの方法については後述する。

出力をみてみよう。

head(design)

  profileID respID qID altID obsID price type_Fuji type_Gala type_Honeycrisp
1        31      1   1     1     1   2.5         1         0               0
2        79      1   1     2     1   4.0         0         0               1
3        51      1   1     3     1   3.5         0         0               1
4         0      1   1     4     1   0.0         0         0               0
5        14      1   2     1     2   3.0         0         1               0
6        67      1   2     2     2   2.5         0         1               0
  freshness_Poor freshness_Average freshness_Excellent no_choice
1              0                 1                   0         0
2              0                 0                   1         0
3              0                 1                   0         0
4              0                 0                   0         1
5              1                 0                   0         0
6              0                 0                   1         0

designはデータフレームで、行は「ある調査対象者にある試行で提示するある選択肢」を表す。よってこの例では100 x 4 x 6 = 2400 行となる。各列は以下を表す。

• profileID: プロファイル番号(「どれも選ばない」プロファイルは0)
• respID: 調査対象者番号
• qID: 試行番号
• altID: 選択肢番号(「どれも選ばない」選択肢は4)
• price: 1パウンドあたり価格の水準
• type_Fuji: 品種の水準がFujiであるとき1,そうでないとき0
• type_Gala: 品種の水準がGalaであるとき1,そうでないとき0
• …
• no_choice: その選択肢が「どれも選ばない」選択肢であるとき1, そうでないとき0

たとえば調査対象者1には、試行1でプロファイル31(2.5, Fuji, Average), 79(4.0, Honeycrisp, Excellent), 51(3.5, Honeycrisp, Average), 0(どれも選ばない)を提示しろ、というわけです。

4 実験計画の特徴を調べる

これから、実験計画を生成するための6個の方法について検討したい。その準備として、実験計画に期待される特徴について考えておこう。

4.1 必須の特徴

選択型コンジョイント分析においては、実験計画は次の特徴を満たしているべきであろう。これらはいわば最低限の条件だといえる。

• 試行内のプロファイル非重複。ある試行の中に同一のプロファイルが出現することはない。たとえば、ある試行における3つの選択肢のうち1つがプロファイル(1, Fuji, Poor)だったら、他の2つの選択肢はそのプロファイルではない。
• 対象者内の試行非重複。ある調査対象者の異なる試行において、全く同一のプロファイルのセットが提示されることはない。たとえば、ある調査対象者のある試行において提示される3つのプロファイルが(1, Fuji, Poor), (2, Gala, Average), (3, Honeycrisp, Excellent) だったとしよう。このとき、この調査対象者の他の試行において提示される3つのプロファイルをよく見たら、あれれ、順序はちがえどこの3つじゃん… ということは起きない。

cbcToolsで生成した実験計画は、どの方法で生成したとしても、上の2つの特徴を持つ(と、cbcToolsパッケージの作者は使用説明書のなかで述べている)。

これら以外の特徴は必ずしも保証されていない。生成される実験計画は、上の2つの特徴を満たしていても、良し悪しの違いがある。調査者は生成された実験計画が良い実験計画になっているか、自分でちゃんと調べる必要があるのです。

4.2 期待される特徴

では、良い実験計画とはなにか。一般に、達成すべき特徴として次の3つが挙げられることが多いと思う。

• 水準の均等性。すなわち、ある属性に注目したとき、各水準が提示される頻度が水準間で等しいこと。たとえば、品種がFujiであるプロファイルが提示される回数と、Galaであるプロファイルが提示される回数が等しい。
• 属性の直交性。すなわち、2つの属性の水準は独立に出現すること。表側に品種、表頭に品質をとった3x3のクロス表をつくったとしよう。Fuji-PoorのセルにはFujiかつPoorであるプロファイルが提示される回数が入る。このクロス表の行をみたとき、行内の3つの値の比率はどの行でも等しく、このクロス表の列を見たとき、列内の3つの値の比率はどの列でも等しい。
• 水準の最小重複。すなわち、水準が同じプロファイルが複数提示される試行ができるだけ少ないこと。たとえば、ある試行の選択肢1として表示されるプロファイルの品種がFujiだとして、選択肢2,3のプロファイルはなるべくFujiでないこと。

これらの特徴が求められる最大の理由は、これらの特徴が失われるとパラメータの推定精度が下がるためである。正確にいうと、属性の直交性と水準の最小重複は属性の主効果しか推定しない場合に求められる特徴であり、もし交互作用効果も推定するのなら、むしろ望ましくない特徴となる。

なお、推定精度以外の理由でこれらの特徴を追求したくなることもある。たとえば、ある店舗での買い物を想定した選択型コンジョイント分析をやるとしよう。属性はブランドと価格の2つ。調査対象者には、下に並んでいる3つの選択肢はその店舗の商品です、買いたいものをひとつ選んでください、と教示する。このとき、ある試行における選択肢のなかに、ブランドが同じで価格が異なる2つの選択肢が含まれていたら、それはかなり奇妙に感じられるだろう。ブランドの重複を禁止したくなる。

4.3 特徴の調べ方

cbcToolsパッケージは、水準の均等性と属性の直交性をチェックするツールとしてcbc_balance(), 水準の重複をチェックするツールとしてcbc_overlap()を用意している。しかし、これらのツールはあくまで全調査対象者を通じた3つの性質を調べているだけだという点に注意する必要がある。全対象者を通じてこの性質が達成できていたとしても、各対象者において達成できているとは限らない。

話が逸れるので深入りしないが、コンジョイント分析の回答を分析する際には、全員のデータを単に積み上げて集団レベルのパラメータを推定する場合と、階層モデルなどをあてはめて個人レベルのパラメータを推測する場合がある。特に後者の場合には、実験計画についても個人レベルで丁寧に調べておく必要があるだろう。

例を挙げよう。 さきほどつくった実験計画について、品種の各水準の出現回数を調べてみる。まずは全対象者を通して調べてみよう。

design %>%
  summarize(
    type_Fuji = sum(type_Fuji), 
    type_Gala = sum(type_Gala), 
    type_Honeycrisp = sum(type_Honeycrisp)
  ) %>%
  print(.)

  type_Fuji type_Gala type_Honeycrisp
1       592       601             607

提示されるプロファイルはのべ 100x3x6=1800個だが、うちFujiは592個、Galaは601個, Honeycrispは607個である。水準の均等性がかなり達成されている。

今度は、各調査対象者について調べてみよう。

design %>%
  group_by(respID) %>%
  summarize(
    type_Fuji = sum(type_Fuji), 
    type_Gala = sum(type_Gala), 
    type_Honeycrisp = sum(type_Honeycrisp)
  ) %>%
  ungroup() %>%
  head(.)

# A tibble: 6 × 4
  respID type_Fuji type_Gala type_Honeycrisp
   <int>     <dbl>     <dbl>           <dbl>
1      1         5         8               5
2      2         6         3               9
3      3         4         9               5
4      4         8         4               6
5      5         3         8               7
6      6         7         3               8

各対象者に提示されるプロファイルはのべ 3x6 = 18個だが、対象者2の場合、うちFujiは6個、Galaは3個、Honeycrispは9個である。水準の均等性を達成できているとは言いがたい。

このように、実験計画の特徴を丁寧に調べることはとても大事である。いっぽう、次のような限界もある。たとえば、「水準の均等性はちょっと崩れているが属性の直交性は達成できている」実験計画と、「水準の均等性は達成できているが属性の直交性はちょっと崩れている」実験計画があるとする。より良い実験計画はどちらか。実験計画の特徴を定性的に観察しているかぎり、こういう問いに答えるのは難しい。

5 実験計画の最適性を調べる

実験計画の個々の特徴に注目するのではなく、その良し悪しを定量的に評価する方法として、最適性という考え方がある。以下ではそのひとつであるD-最適性、そしてその発展形であるDB-最適性という概念について説明する。この説明は、cbcToolsパッケージが提供する6種類の実験計画生成方法のうちdopt, CED, Modfedに関わる。

5.1 計画行列

話を思い切り簡単にして、2属性、2x3水準の実験計画について考える。

profiles_2x3 <- cbc_profiles(
  A = c('A1', 'A2'),
  B = c('B1', 'B2', 'B3')
)
print(profiles_2x3)

  profileID  A  B
1         1 A1 B1
2         2 A2 B1
3         3 A1 B2
4         4 A2 B2
5         5 A1 B3
6         6 A2 B3

ありうるプロファイルは6個。これらのプロファイルを数値で表現する方法について考えよう。ある水準を持っていることを1, 持っていないことを0として、次のように表現できる。

profiles_2x3 %>%
  makedummies(as.is = TRUE) %>%
  print(.)

  profileID A B_B2 B_B3
1         1 0    0    0
2         2 1    0    0
3         3 0    1    0
4         4 1    1    0
5         5 0    0    1
6         6 1    0    1

Aは、属性AがA2だったときに1、そうでないときに0となる変数。B_B2は、属性BがB2だったときに1、そうでないときに1となる変数。B_B3は、属性BがB3だったときに1、そうでないときに1となる変数。この3列があれば十分である。たとえば「属性BがB1だったときに1、そうでないときに0となる変数」はいらない(B_B2とB_B3をみればわかるから)。

ここからは、選択型コンジョイント分析ではなく、次のような評価型コンジョイント分析について考えよう。ひとりの対象者にあるプロファイルを見せて、(たとえば)そのプロファイルが好きな程度を100点満点で評価してもらう。これを繰り返す。このとき、対象者にはどのプロファイルを見せるべきか。

得られたデータを分析する局面について考える。もっとも単純に、次のような分析方法を考えよう。ある対象者について、プロファイルに対する評価値を目的変数とし、そのプロファイルが持っている水準を説明変数とした線形回帰分析を行う。モデルはこんな感じになる。 \(j\)番目に見せたプロファイルへの評価値を\(y_j\)、そのプロファイルが持っている水準を表す3つの二値変数を\(x_{j1}, x_{j2}, x_{j3}\)として、 \[ y_j = \beta_0 + \beta_{1} x_{j1} + \beta_{2} x_{j2} + \beta_{3} x_{j3} + e_j \] ひとりの人にすべてのプロファイルを上表の順にみせ、評価値\(y_1, \ldots, y_6\)を得たとしよう。モデルはこうなる。 \[ y_1 = \beta_0 + \beta_1 \times 0 + \beta_2 \times 0 + \beta_3 + 0 + e_1 \] \[ y_2 = \beta_0 + \beta_1 \times 1 + \beta_2 \times 0 + \beta_3 + 0 + e_2 \] \[ y_3 = \beta_0 + \beta_1 \times 0 + \beta_2 \times 1 + \beta_3 + 0 + e_3 \] \[ y_4 = \beta_0 + \beta_1 \times 1 + \beta_2 \times 1 + \beta_3 + 0 + e_4 \]

\[ y_5 = \beta_0 + \beta_1 \times 0 + \beta_2 \times 0 + \beta_3 + 1 + e_5 \] \[ y_6 = \beta_0 + \beta_1 \times 1 + \beta_2 \times 0 + \beta_3 + 1 + e_6 \]

行列で書いてみよう。 \[ \left[ \begin{array}{c} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \\ y_6 \end{array} \right] = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} \beta_0 \\ \beta_1 \\ \beta_2 \\ \beta_3 \end{array} \right] + \left[ \begin{array}{c} e_1 \\ e_2 \\ e_3 \\ e_4 \\ e_5 \\ e_6 \end{array} \right] \] これをさらに簡略に \[ \mathbf{y} = \mathbf{X} \mathbf{\beta} + \mathbf{e} \] と書くこともできる。\(\mathbf{X}\)は、すべてのプロファイルを表す表の左に、すべての値が1である列をくっつけた行列である。これを計画行列と呼ぶ。

5.2 最適計画

いま考えたいことは、調査対象者に提示するプロファイルの選び方、つまり、計画行列の行をうまく減らす方法だといえる。しかし、もう少しお待ち下さい。その前に、計画行列の良し悪しを評価する方法について考えたい。

説明のために、架空データに対して線形回帰モデルをあてはめてみよう。

もし正解が\(\beta_0 = 2, \beta_1 = 3, \beta_2 = 2, \beta_3 = 1\)で、撹乱項\(e_1, \ldots, e_6\)の実現値がすべて0ならば、評価値は\(y_1\)から順に\(2, 5, 4, 7, 3, 6\)となる。これにちょっぴりノイズを加えた架空データに対して、線形回帰モデルをあてはめる。

df <- tibble(
  y = c(3,5,4,7,3,6),  # y_1を2から3に変えました
  x1 = c(0,1,0,1,0,1), 
  x2 = c(0,0,1,1,0,0), 
  x3 = c(0,0,0,0,1,1)
)
mod <- lm(y ~ x1+x2+x3, data = df)
summary(mod)

Call:
lm(formula = y ~ x1 + x2 + x3, data = df)

Residuals:
      1       2       3       4       5       6 
 0.3333 -0.3333 -0.1667  0.1667 -0.1667  0.1667 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)   2.6667     0.3333   8.000   0.0153 *
x1            2.6667     0.3333   8.000   0.0153 *
x2            1.5000     0.4082   3.674   0.0667 .
x3            0.5000     0.4082   1.225   0.3453  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4082 on 2 degrees of freedom
Multiple R-squared:  0.975, Adjusted R-squared:  0.9375 
F-statistic:    26 on 3 and 2 DF,  p-value: 0.03726

\(\beta_0\)から順に、\(2.67, 2.67, 1.50, 0.50\)と推定された。

ここで注目したいのは、パラメータの推定値そのものではなく、その推定の精度である。どうせなら、精度の高い推定ができると嬉しいですよね。

精度を知るためのひとつの注目点は、各パラメータの推定の標準誤差である。上の例では、\(0.33, 0.33, 0.41, 0.41\)となっている。もうひとつの注目点は、パラメータの間での推定の共分散である。たとえば、「\(\beta_1\)の推定値がうっかり大きめになってしまったとき、\(\beta_2\)の推定値もつられて大きめになる」なんて性質があったら嫌だけど、共分散はそういう性質を表現している。

Rのlm()関数でつくったオブジェクトの場合、パラメータの推定の共分散はvcov()関数で得られる。

vcov(mod)

            (Intercept)            x1            x2            x3
(Intercept)  0.11111111 -5.555556e-02 -8.333333e-02 -8.333333e-02
x1          -0.05555556  1.111111e-01  5.665583e-18  5.665583e-18
x2          -0.08333333  5.665583e-18  1.666667e-01  8.333333e-02
x3          -0.08333333  5.665583e-18  8.333333e-02  1.666667e-01

4つのパラメータの共分散は4x4の行列として表現される。さきほどチェックした、各パラメータの推定の標準誤差は、この行列の対角成分の平方根である。確かめよう。

sqrt(diag(vcov(mod)))

(Intercept)          x1          x2          x3 
  0.3333333   0.3333333   0.4082483   0.4082483 

ほんとだ、lm()の出力に一致している。そういうわけで、パラメータの推定の共分散行列だけに注目すればよい。この行列の要素がおしなべて小さいと嬉しいわけである。

回帰分析の教科書に書いてあるけど、パラメータの推定の共分散行列\(Var(\beta)\)は次の式で求められる。撹乱項の分散を\(\sigma^2\)として \[ Var(\beta) = \sigma^2 (\mathbf{X}^\top \mathbf{X})^{-1}\] 確かめてみよう。

sigmasq <- var(c(1,0,0,0,0,0))
X <- matrix(
  c(
    1 , 0 , 0 , 0 ,
    1 , 1 , 0 , 0 ,
    1 , 0 , 1 , 0 ,
    1 , 1 , 1 , 0 ,
    1 , 0 , 0 , 1 ,
    1 , 1 , 0 , 1
  ), 
  byrow = TRUE, 
  nrow = 6
)
sigmasq * solve(t(X) %*% X)

            [,1]        [,2]        [,3]        [,4]
[1,]  0.11111111 -0.05555556 -0.08333333 -0.08333333
[2,] -0.05555556  0.11111111  0.00000000  0.00000000
[3,] -0.08333333  0.00000000  0.16666667  0.08333333
[4,] -0.08333333  0.00000000  0.08333333  0.16666667

指数表記のせいでちょっとわかりづらいが、vcov()の出力とほぼ同じ行列になっている。

さて、共分散行列の式から次の2点がわかる。パラメータの共分散行列の要素の値は、

• 撹乱項の分散\(\sigma^2\)が小さいときに小さくなり、
• 計画行列を\(\mathbf{X}\)として、\((\mathbf{X}^\top \mathbf{X})^{-1}\)の要素の値が小さいときに小さくなる。

前者はデータを取ってみないとわからない話だが、後者は計画行列\(\mathbf{X}\)のみによって決まることに注目されたい。つまり、前項では良い実験計画の基準として、水準の均等性・属性の直交性・水準の最小重複という定性的な特徴に注目したが、そういう話を全部すっ飛ばし、単に、\((\mathbf{X}^\top \mathbf{X})^{-1}\)の要素の値がおしなべて小さくなるような実験計画を作ればいいじゃん、という考え方もできるのである。実験計画法の世界では、この考え方を最適計画という。

5.3 D-最適性

では、\((\mathbf{X}^\top \mathbf{X})^{-1}\)の要素の値の全体的な小ささをどうやって評価すればよいか。

いろんな評価方法があり得る。もっともポピュラーなのは、\(\mathbf{X}\)の行数を\(n\)として、\(\mathbf{X}^\top \mathbf{X}/n\)の行列式\(|\mathbf{X}^\top \mathbf{X}/n|\)に基づく指標を使うという方法である。この指標が大きいと嬉しい。これを実験計画のD-最適性という。

上の例の計画行列\(\mathbf{X}\)についてD-最適性を求めてみよう。 まずは、AlgDesignパッケージのevals.design()という関数を使ってみる。 このパッケージは、\(\mathbf{X}\)の列数を\(k\)として\(|\mathbf{X}^\top \mathbf{X}/n|^{1/k}\)をD-最適性としている。

print(eval.design(~., design = profiles_2x3[-1]))

$determinant
[1] 0.3102016

$A
[1] 5

$diagonality
[1] 0.874

$gmean.variances
[1] 5.241483

要素determinantにd-最適性が格納されている。

今度は自力で求めてみよう。

det(t(X) %*% X / 6) ^ (1/4)

[1] 0.3102016

ほんとだ、一致する。

なお、もし行列の固有値という概念がおなじみならば、 行列式とは固有値の積だということを思いだしてくださってもよい。つまり、上記のd-最適性は、 \(\mathbf{X}^\top \mathbf{X} /n\)の固有値の幾何平均だともいえる。

prod(eigen(t(X) %*% X / 6)$value) ^ {1/4}

[1] 0.3102016

というわけで、この値が大きい方が嬉しいわけである。ためしに、計画行列から最後の行を取り除いてみよう。水準の均等性も属性の直交性も崩れてしまうから、D-最適性は下がるはずである。

det(t(X[-6,]) %*% X[-6,] / 6) ^ (1/4)

[1] 0.2357023

ほんとだ、少し小さくなった。

よしわかった、D-最適性が大きい実験計画が良い実験計画だ！ ということで話を終わらせたいのはやまやまだが、そうは問屋が卸さない。先ほど述べたように、実験計画のD-最適性という概念は線形回帰モデルに基づいている。いっぽう、いま注目しているのは選択型コンジョイント分析であり、残念ながら、選択型コンジョイント分析においてはふつう線形回帰モデルは用いられない。線形回帰モデルにおけるD-最適性を最大化する実験計画が、選択型コンジョイント分析においても良い計画だとは言い切れないのである。

5.4 多項ロジットモデルの計画行列

今度は選択型コンジョイント分析における実験計画の最適性について考えてみよう。

再び、2属性、2x3水準の実験計画について考える。ありうるプロファイルの数は6個。調査対象者はひとり、試行数は6、選択肢数は3とする。

次の実験計画を用いたとしよう。

set.seed(123)
demo2 <- cbc_design(
  profiles = profiles_2x3,
  n_resp   = 1,    
  n_alts   = 3,    
  n_q      = 6,    
  no_choice = FALSE,  
  method   = 'full'  
)
head(demo2)

  profileID respID qID altID obsID  A  B
1         5      1   1     1     1 A1 B3
2         4      1   1     2     1 A2 B2
3         3      1   1     3     1 A1 B2
4         2      1   2     1     2 A2 B1
5         3      1   2     2     2 A1 B2
6         6      1   2     3     2 A2 B3

選択型コンジョイント分析では、多くの場合、パラメータの推定に多項ロジットモデルが用いられる。以下のようなモデルである。説明を簡単にするために、あるひとりの選択について考える。

まず、各プロファイルは各試行において選ばれやすさを持っていると考える。試行\(j\), 選択肢\(k\)のプロファイルの選ばれやすさを\(u_{jk}\)とする。

個々のプロファイルの選ばれやすさは、そのプロファイルが持っている水準の選ばれやすさ(部分効用)の合計(全体効用)にノイズが載ったものだと考える。

プロファイルを表す3つの二値変数を\(x_{jk1}, x_{jk2}, x_{jk3}\)として、 \[ u_{jk} = \beta_{1} x_{jk1} + \beta_{2} x_{jk2} + \beta_{3} x_{jk3} + e_{jk} \] \(\beta_{1}\)は「属性Aの水準がA2であることの部分効用」を表している(A1であることの部分効用を0としている)。同様に、\(\beta_{2}, \beta_{3}\)は「属性Bの水準がB2であることの部分効用」、「B3であることの部分効用」を表している(B1であることの部分効用を0としている)。さきほどの線形回帰モデルとの違いは次の3点である。

• 添え字が増えた。
• 左辺が評価値\(y_j\)ではなくて観察されない変数\(u_{jk}\)になった。
• 切片項\(\beta_0\)が不要になった。観察されるのは\(u_{jk}\)そのものではなく、それらを試行内で比較したうえでの対象者の選択だから、\(\beta_0\)は省いてかまわない。

さきほどと同様に簡略化して、 \[ \mathbf{u} = \mathbf{X} \mathbf{\beta} + \mathbf{e}\] と書くこともできる。\(\mathbf{u}\)は\(u_{11}, u_{12}, ...\)を縦に並べたベクトル。計画行列\(\mathbf{X}\)は、18行もあるので書きませんけど、その1行目はプロファイル(A1, B3)だから\((0, 0, 1)\)である。さきほどと違い3列になる。

最後に、対象者は試行\(j\)において、選ばれやすさ\(u_{jk}\)がもっとも高い選択肢\(k\)を選ぶと考える。撹乱項\(e_{jk}\)についてある仮定を置くと、これは結局次の式で表現される。対象者が試行\(j\)において\(k\)を選ぶ確率を\(p_{jk}\)とし、\(u_{jk}\)から\(e_{jk}\)を取り除いた部分を\(v_{jk}\)として、 \[ p_{jk} = \frac{\exp(v_{jk})}{\exp(v_{j1})+\exp(v_{j2})+\exp(v_{j3})} \] 指数関数のせいでややこしく見えるけれど、要は、ある選択肢が選ばれる確率は、その選択肢の全体効用の相対的な大きさで決まる、ということである。

5.5 多項ロジットモデルにおける最適計画

説明のために、架空データに対して多項ロジットモデルをあてはめてみよう。

まず、架空データをつくる。パラメータは\(\beta_1 = 3, \beta_2 = 2, \beta_3 = 1\)としよう。

set.seed(123)
dfData_demo2 <- demo2 %>%
  dplyr::select(respID, qID, altID, A, B) %>%
  makedummies(.) %>% 
  mutate(
    v = A * 3 + B_B2 * 2 + B_B3 * 1, 
    expv = exp(v)
  ) %>%
  group_by(respID, qID) %>%
  mutate(
    prob = expv / sum(expv) 
  ) %>%
  ungroup() %>%
  dplyr::select(-expv)
dfChoice <- dfData_demo2 %>%
  group_by(respID, qID) %>%
  summarize(nChoice = sample(altID, 1, prob = prob)) %>%
  ungroup() 
dfData_demo2 <- dfData_demo2 %>%
  left_join(dfChoice, by = c("respID", "qID")) %>%
  mutate(bChoice = if_else(nChoice == altID, 1, 0)) %>%
  dplyr::select(-nChoice) 
head(dfData_demo2)

# A tibble: 6 × 9
  respID   qID altID     A  B_B2  B_B3     v   prob bChoice
   <int> <int> <int> <int> <int> <int> <dbl>  <dbl>   <dbl>
1      1     1     1     0     0     1     1 0.0171       0
2      1     1     2     1     1     0     5 0.936        1
3      1     1     3     0     1     0     2 0.0466       0
4      1     2     1     1     0     0     3 0.245        1
5      1     2     2     0     1     0     2 0.0900       0
6      1     2     3     1     0     1     4 0.665        0

たとえば、試行1の3つの選択肢の全体効用(v)は、選択肢1から順に\(1, 5, 2\)となる。これを確率(prob)にすると、\(0.017, 0.936, 0.046\) である。この確率に従って選択肢をひとつ選んだところ(bChoice)、選択肢2が選ばれた。このように、すべての試行について架空の選択データを得た。

このデータに多項ロジットモデルをあてはめてみよう。mlogitパッケージを使う。

dfData_mlogit <- dfidx(
  dfData_demo2 %>% mutate(respID_qID = respID * 10 + qID), 
  idx = c("respID_qID", "altID")
)
oMlogit <- mlogit(bChoice ~ 0 + A + B_B2 + B_B3, data = dfData_mlogit)
summary(oMlogit)

Call:
mlogit(formula = bChoice ~ 0 + A + B_B2 + B_B3, data = dfData_mlogit, 
    method = "nr")

Frequencies of alternatives:choice
      1       2       3 
0.33333 0.50000 0.16667 

nr method
5 iterations, 0h:0m:0s 
g'(-H)^-1g = 1.37E-06 
successive function values within tolerance limits 

Coefficients :
     Estimate Std. Error z-value Pr(>|z|)
A     1.89323    1.22909  1.5404   0.1235
B_B2 -0.49409    1.43124 -0.3452   0.7299
B_B3 -0.19449    1.14973 -0.1692   0.8657

Log-Likelihood: -4.9116

パラメータの推定値は、\(\beta_1, \beta_2, \beta_3\)の順に\(1.89, -0.49, -0.19\)となった。正解からかなりずれているが、なにしろ1人・6試行のデータしかないので、仕方がないだろう。

例によって、注目したいのはパラメータ推定値そのものではなくその推定精度である。パラメータの推定の共分散行列を調べてみよう。

vcov(oMlogit)

               A       B_B2        B_B3
A     1.51066044 -0.6279408 -0.08761228
B_B2 -0.62794075  2.0484439  0.54847004
B_B3 -0.08761228  0.5484700  1.32189011

この行列の要素がおしなべて小さいと嬉しいわけである。

ところで、多項ロジットモデルのパラメータの推定の共分散行列\(Var(\beta)\)は次の式で求められるのだそうです。試行\(j\)における選択肢1, 2, 3の選択確率を\(p_{j1}, p_{j2}, p_{j3}\)とし、ベクトルにして\(\mathbf{p}_j = (p_{j1}, p_{j2}, p_{j3})^\top\)とする。このベクトルを対角成分に持つ対角行列を\(\mathbf{P}_j\)とする。計画行列から試行\(j\)の3行を切り出した行列を\(\mathbf{X}_j\)とする。 \[ Var(\beta) = \left( \sum_{j=1}^J \mathbf{X}_j^\top (\mathbf{P}_j - \mathbf{p}_j \mathbf{p}^\top_j ) \mathbf{X}_j \right)^{-1}\]

ほんとかな？ 確かめてみよう。

agCoef <- coef(oMlogit)
dfTemp <- demo2 %>%
  dplyr::select(respID, qID, altID, A, B) %>%
  makedummies(.) %>% 
  mutate(
    v = A * agCoef[1] + B_B2 * agCoef[2] + B_B3 * agCoef[3], 
    expv = exp(v)
  ) %>%
  group_by(respID, qID) %>%
  mutate(
    prob = expv / sum(expv) 
  ) %>%
  ungroup() %>%
  dplyr::select(-expv)
lTemp <- lapply(
  split(dfTemp, list(dfTemp$respID, dfTemp$qID)), 
  function(dfIn){
    X <- dfIn %>% dplyr::select(A, B_B2, B_B3) %>% as.matrix(.)
    p <- dfIn %>% pull(prob)
    t(X) %*% (diag(p) - p %*% t(p)) %*% X
  }
)
out <- matrix(0, ncol = 3, nrow = 3)
for (i in seq_along(lTemp))
  out <- out + lTemp[[i]]
out <- solve(out)
print(out)

               A       B_B2        B_B3
A     1.51065970 -0.6279402 -0.08761234
B_B2 -0.62794022  2.0484433  0.54847001
B_B3 -0.08761234  0.5484700  1.32189004

おおおお！ ほんとだーーーー！ (感動)

さて、ここで計画行列の最適性について考えてみよう。

線形回帰モデルの場合、パラメータの共分散行列は\[ Var(\beta) = \sigma^2 (\mathbf{X}^\top \mathbf{X})^{-1} \] であった。この式は、データを取らないとわからない部分\(\sigma^2\)と、計画行列だけで決まる部分\(\mathbf{X}^\top \mathbf{X}\)に分けられる。そこで、\(|\mathbf{X}^\top \mathbf{X}|^{1/k}\)をD-最適性と呼ぶことにしたのであった。

ところが多項ロジットモデルの場合、パラメータの共分散行列は \[ Var(\beta) = \left( \sum_{j=1}^J \mathbf{X}_j^\top (\mathbf{P}_j - \mathbf{p}_j \mathbf{p}^\top_j ) \mathbf{X}_j \right)^{-1}\] という式になっている。計画行列\(\mathbf{X}\)で決まる部分と、データを取ってみないとわからない部分\(\mathbf{P}_j - \mathbf{p}_j \mathbf{p}^\top_j\)を切り分けることができない。つまり、実験計画の最適性を計画行列だけで決めることができないのである。

これは困りましたね…

5.6 DB-最適性

そこで登場するのがDB-最適性という概念である。

まず、パラメータ数を\(k\)として、\(|Var(\beta)|^{1/k}\)をD-誤差と呼ぶことにする。もちろん小さい方が嬉しい。

先程述べた理由で、多項ロジットモデルのD-誤差は計画行列だけでは決まらない。しかし、もしもデータを取る前にパラメータ\(\beta\)を仮に決めることができたら、そこから\(\mathbf{p}_j\)を求めることで、その\(\beta\)のもとでのD-誤差を求めることはできる。

そこで、パラメータ\(\beta\)がどんな値を取りそうかという点についてなんらかアタリをつけ、それを確率分布\(\pi(\beta)\)として表現する。これを事前分布と呼ぶ。で、この分布を通じてD-誤差を平均する。 \[ \int |Var(\beta)|^{1/k} \pi(\beta) d \beta\] これをベイジアンD-誤差、略してDB-誤差という。

このDB-誤差を最小化する計画行列を使えばよいではないか。というのが、DB-最適性という考え方である。

上の例の計画行列について、DB-誤差を求めてみよう。idefixパッケージのDBerr()関数を使う。

まず事前分布を決めよう。調査者がパラメータ\(\beta_1, \beta_2, \beta_3\)について、データを取る前から、それはだいたい\(3, 2, 1\)なんじゃないかしらん、と薄々感じていたとしよう。さらに、たとえば\(\beta_1\)は\(3\)より大きいかもしれないし小さいかもしれないし、\(\beta_2\)も\(2\)より大きいかもしれないし小さいかもしれないけれど、\(\beta_1\)が\(3\)より大きいかどうかと、\(\beta_2\)が\(2\)より大きいかどうかとの間には関係がない… という風に考えていたとしよう。

この調査者が胸に抱いている\(\beta\)についての事前のアタリのようなものを、多変量正規分布 \[ MVN \left( \left[ \begin{array}{c} 3 \\ 2 \\ 1 \end{array} \right], \left[ \begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{array} \right] \right) \] で表現することにする。共分散行列の対角要素\(2\)は、調査者の確信の強さを表している(大きいほうが確信が低い)。「まったくわかりません」ということを 表現したい場合は、平均を0とし分散を大きくするのがよいだろう。

set.seed(123)
mgPrior <- MASS::mvrnorm(100, c(3,2,1), 2*diag(3)) 

せっかくなのでこの事前分布を視覚化してみよう。GGallyパッケージを使う。

colnames(mgPrior) <- c("beta_1", "beta_2", "beta_3")
ggpairs(as.data.frame(mgPrior))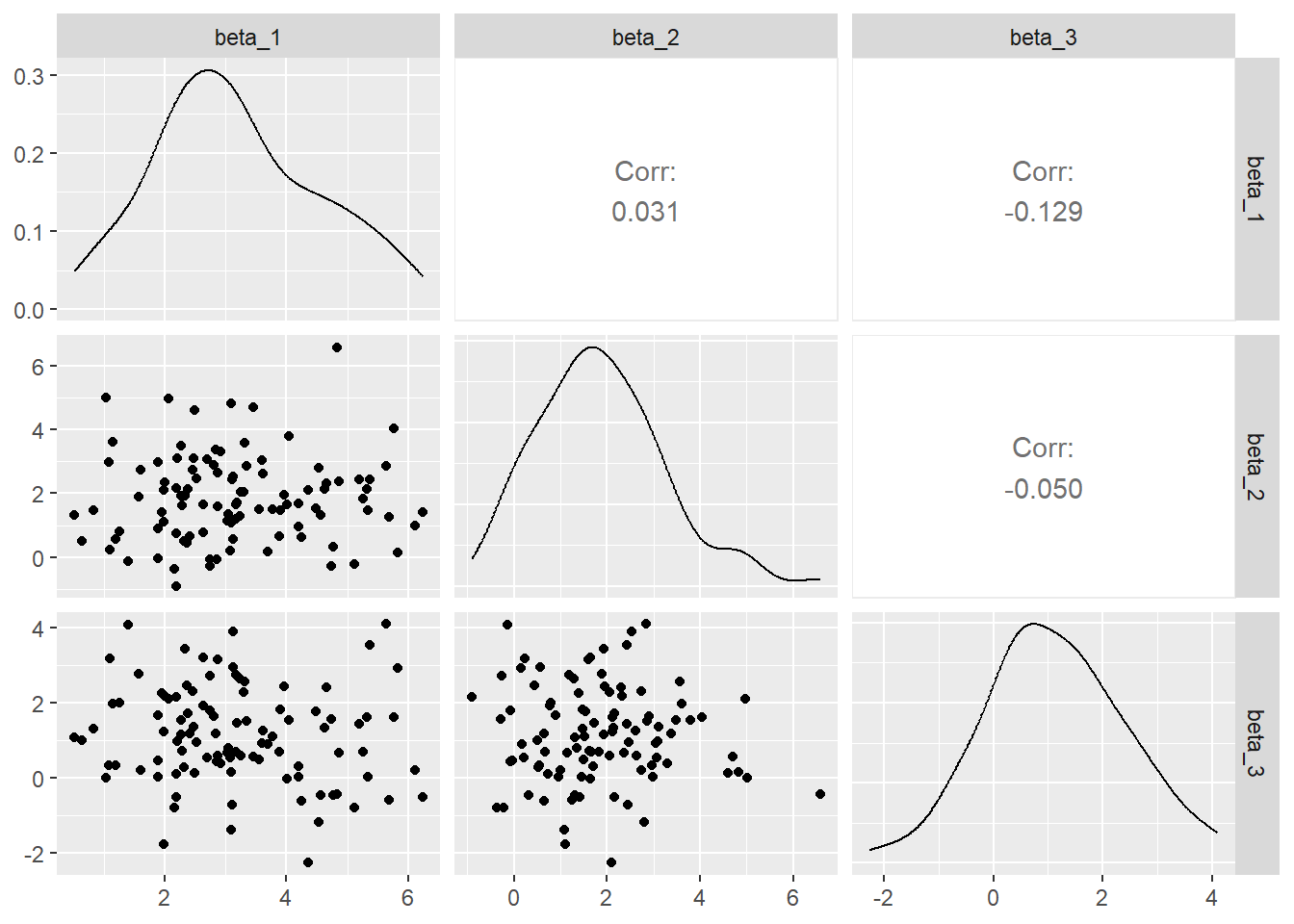

たとえば左下のパネルは\(\beta_1\)と\(\beta_3\)の同時分布である。\(\beta_1\)は3のまわりに、\(\beta_3\)は1のまわりに散らばっている。この事前分布によって、調査者は自分の事前の想定・知識を表現しているわけである。

この事前分布のもとでの、計画行列のDB-誤差を求めよう。

set.seed(123)
X <- demo2 %>%
  makedummies(.) %>% 
  dplyr::select(A, B_B2, B_B3) %>%
  as.matrix(.)
DBerr(mgPrior, X, n.alts = 3)

[1] 4.420208

DB-誤差は4.42となった。ためしに計画行列を1行削ってみよう。DB-誤差は大きくなるはずである。

DBerr(mgPrior, X[-(1:3),], n.alts = 3)

[1] 5.099887

少し大きくなった。

このDB-最適性という考え方の辛いところは、いうまでもなく、調査者がコンジョイント分析を行う前にパラメータの値についてのある程度の知識を持ち、それを確率分布の形で表現しなければならない、という点である。idefixパッケージの作者たちは、事前の情報の集め方として、文献を調べる、パイロット調査をやる、専門家に訊いたりフォーカス・グループ・インタビューをやる… といった方法を挙げている。

6 実験計画の生成方法

お待たせしました。ここからは、cbcToolsが提供する6個の生成方法(random, full, orthogonal, dopt, CED, Modfed)について検討する。

6.1 random

いわゆるランダム法。

引き続き、2属性、2x3水準の実験計画について考える。ありうるプロファイル数は2x3=6である。 調査対象者数は10, 試行あたり選択肢数は3, 調査対象者あたり試行数は4とする。「どれも選ばない」は提示しない。生成すべき実験計画は10x3x4 = 120行となる。

set.seed(123)
demo_random <- cbc_design(
  profiles = profiles_2x3,
  n_resp   = 10,       # 調査対象者数
  n_alts   = 3,        # 試行あたり選択肢数。ただし「どれも選ばない」は除く
  n_q      = 4,        # 調査対象者あたり試行数
  no_choice = FALSE,   # 「どれも選ばない」を含めない
  method   = 'random'  # 実験計画の生成方法
)

ソースコードを調べると( cbcTools:::make_design_random() )、実験計画は次のように生成されているようだ。

1. ありうるプロファイル(ここでは6個)から、(調査対象者数)x(試行数)x(選択肢数)個を等確率で復元抽出する(ここでは120個)。
2. 得られた行のうち、試行のなかでプロファイルが重複している試行、ならびに、全く同一のプロファイルを提示する複数の試行を持っている調査対象者を特定し、それに相当する行を特定する。
3. 2で特定した行数だけ、再度復元抽出を行い、2で特定した行を上書きする。
4. 2で特定した行数が0になるまで、2と3を繰り返す。

生成された実験計画をみてみよう。

demo_random %>% 
  dplyr::select(respID, qID, altID, profileID) %>%
  pivot_wider(names_from = c(qID, altID), values_from = profileID) %>%
  print(.)

# A tibble: 10 × 13
   respID `1_1` `1_2` `1_3` `2_1` `2_2` `2_3` `3_1` `3_2` `3_3` `4_1` `4_2`
    <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
 1      1     3     1     2     2     5     6     3     5     4     4     6
 2      2     2     3     5     1     2     5     5     3     1     4     2
 3      3     2     1     6     3     4     6     1     3     5     4     2
 4      4     6     2     1     3     4     5     5     3     6     1     2
 5      5     2     5     3     2     3     1     3     1     6     5     1
 6      6     1     5     2     1     6     3     4     3     5     3     2
 7      7     6     1     2     6     3     1     4     6     1     6     5
 8      8     6     4     1     3     1     4     6     5     3     6     2
 9      9     5     3     2     1     6     5     3     5     4     5     2
10     10     1     4     2     4     5     1     3     6     1     3     5
# ℹ 1 more variable: `4_3` <int>

上の出力は、行が調査対象者、行が試行x選択肢(たとえば1_2は試行1の選択肢2)、値がプロファイル番号である。 実験計画は調査対象者によって異なっていることがわかる。

この手法では、水準の均等性、属性の直交性、水準の最小重複のいずれの特徴についても、特段の注意が払われていない。上の実験計画についてこの3つの特徴を調べてみよう。

まず水準の均等性から。対象者別に各水準の提示回数を調べてみる。

demo_random %>%
  dplyr::select(respID, A, B) %>%
  pivot_longer(cols = c(A, B), names_to = "attribute", values_to = "level") %>%
  group_by(respID, level) %>%
  summarize(freq = n()) %>%
  ungroup() %>%
  pivot_wider(names_from = level, values_from = freq) %>%
  print(.)

# A tibble: 10 × 6
   respID    A1    A2    B1    B2    B3
    <int> <int> <int> <int> <int> <int>
 1      1     5     7     4     4     4
 2      2     7     5     5     3     4
 3      3     6     6     4     4     4
 4      4     7     5     4     3     5
 5      5     8     4     6     3     3
 6      6     8     4     4     4     4
 7      7     6     6     4     3     5
 8      8     6     6     3     4     5
 9      9     8     4     4     3     5
10     10     7     5     5     4     3

ひとりあたりの提示プロファイルは延べ 3x4 = 12個である。たとえば属性Aについては、12個中6個がA1, 6個がA2になっていてほしい。しかし、この実験計画ではかなりのばらつきが生じている。対象者1では、12個中5個がA1, 7個がA2になっている。

属性の直交性はどうか。対象者別に、各プロファイルの提示回数を調べてみよう。

demo_random %>%
  dplyr::select(respID, A, B) %>%
  group_by(respID, A,B) %>%
  summarize(freq = n()) %>%
  ungroup() %>%
  pivot_wider(names_from = c(A, B), values_from = freq) %>%
  print(.)

# A tibble: 10 × 7
   respID A1_B1 A1_B2 A1_B3 A2_B1 A2_B2 A2_B3
    <int> <int> <int> <int> <int> <int> <int>
 1      1     1     2     2     3     2     2
 2      2     2     2     3     3     1     1
 3      3     2     2     2     2     2     2
 4      4     2     2     3     2     1     2
 5      5     3     3     2     3    NA     1
 6      6     2     3     3     2     1     1
 7      7     3     2     1     1     1     4
 8      8     2     2     2     1     2     3
 9      9     2     2     4     2     1     1
10     10     3     2     2     2     2     1

属性の直交性が達成されていれば、属性Aが水準A1である提示刺激における属性Bの水準の構成比と、A2である提示刺激における属性Bの水準の構成比が等しくなるはずである。しかしこの実験計画ではそうなっていない。調査対象者5にいたっては、水準A1とB2の組み合わせは3回提示されているのに、水準A2とB2の組み合わせは一度も提示されていない。

水準の重複はどうか。対象者x属性別に、使用された水準数別の試行数を調べてみよう。

demo_random %>%
  dplyr::select(respID, qID, A, B) %>%
  pivot_longer(cols = c(A, B), names_to = "attribute", values_to = "level") %>%
  group_by(respID, qID, attribute) %>%
  summarize(n_usedlevel = length(unique(level))) %>%
  ungroup() %>%
  group_by(respID, attribute, n_usedlevel) %>%
  summarize(freq = n()) %>%
  ungroup() %>%
  pivot_wider(names_from = c(attribute, n_usedlevel), values_from = freq) %>%
  print(.)

# A tibble: 10 × 5
   respID   A_1   A_2   B_2   B_3
    <int> <int> <int> <int> <int>
 1      1     1     3     3     1
 2      2     2     2     1     3
 3      3     1     3     2     2
 4      4    NA     4     4    NA
 5      5    NA     4     2     2
 6      6    NA     4     2     2
 7      7    NA     4     2     2
 8      8    NA     4     3     1
 9      9    NA     4     3     1
10     10    NA     4     1     3

上の集計はちょっとわかりにくいが、たとえばA_2列は、「その調査対象者の4試行のうち、選択肢の中に属性Aの2つの水準のうちすべてが登場する試行は何試行か」を示している。水準の最小重複とは、A_2, B_3の列の値ができるだけ大きいということを指す。

この例では、たとえば調査対象者1の4試行のうち、Aの2つの水準をすべて使った試行は3試行であり、残りの1試行では、Aの水準は1個しか使われていない。調査対象者1の実験計画を調べてみよう。

demo_random %>%
  dplyr::filter(respID == 1) %>%
  print(.)

   profileID respID qID altID obsID  A  B
1          3      1   1     1     1 A1 B2
2          1      1   1     2     1 A1 B1
3          2      1   1     3     1 A2 B1
4          2      1   2     1     2 A2 B1
5          5      1   2     2     2 A1 B3
6          6      1   2     3     2 A2 B3
7          3      1   3     1     3 A1 B2
8          5      1   3     2     3 A1 B3
9          4      1   3     3     3 A2 B2
10         4      1   4     1     4 A2 B2
11         6      1   4     2     4 A2 B3
12         2      1   4     3     4 A2 B1

第4試行で、3つの選択肢のすべてがA2になっている。

6.2 full

full factorial design(完全要因実施計画) の略。完全要因実施計画とは実験計画法の用語で、ここでは「ありうるすべてのプロファイルを提示する」ことに相当する。

引き続き、2属性、2x3水準とする。ありうるプロファイル数は2x3=6である。調査対象者数10, 試行あたり選択肢数3, 調査対象者あたり試行数4、「どれも選ばない」提示なし、とする。生成すべき実験計画は10x3x4 = 120行となる。

set.seed(123)
demo_full <- cbc_design(
  profiles = profiles_2x3,
  n_resp   = 10,      # 調査対象者数
  n_alts   = 3,       # 試行あたり選択肢数。ただし「どれも選ばない」は除く
  n_q      = 4,       # 調査対象者あたり試行数
  no_choice = FALSE,  # 「どれも選ばない」を含めない
  method   = 'full'   # 実験計画の生成方法
)

ソースコードを調べると( cbcTools:::make_design_full() )、実験計画は次の手順で生成されているようだ。

1. すべてのプロファイルをランダムに並べ替え、行番号をつける。上の例では6行。
2. 1.を選択肢数だけ繰り返し、出来上がった(選択肢数)個の行列を縦に積み上げ、1.でつけた行番号でソートする。上の例では6x3 = 18行。
3. こうしてできた行列をある1人の調査対象者の実験計画とみなして、上から順に、試行1の選択肢1, 2, …, 試行2の選択肢1, 2, …とする。 つまりこの段階では、ある選択肢番号についてみると、全試行を通じてプロファイルに重複がない。なお、ここで作成した実験計画の試行数は実際の試行数とは異なる。上の例では実際の試行数は4であり、必要なプロファイル数は4x3=12なのだが、この行列は18行あるので、最後の行は試行6となる。
4. もし、試行のなかでプロファイルが重複している試行、ならびに、全く同一のプロファイルを提示する複数の試行が存在したら、この行列を丸ごと捨てて、1.からやり直す。
5. この行列を調査対象者数だけ複製し、縦に積み上げる。上の例では180行。
6. この行列の上から、(調査対象者数x試行数x選択肢数)行を取り出す。上の例では10x3x4 = 120行。
7. こうしてできた行列を、(調査対象者数)人ぶんの実験計画とみなし、試行番号を振り直す。上から順に、調査対象者1の試行1の選択肢1, 2, …, 試行2の…, 調査対象者2の試行1の, … となる。

この生成方法の挙動は、元のプロファイル数と試行数との大小で変わってくる。3つのケースに分けて考えよう。

• ケース1, ありうるプロファイル数が試行数より大きい場合。上記のコード例がそうである。ふつうありうるプロファイル数は多いから、たいていの場合はこのケースでしょうね。

demo_full %>% 
  dplyr::select(respID, qID, altID, profileID) %>%
  pivot_wider(names_from = c(qID, altID), values_from = profileID) %>%
  print(.)

# A tibble: 10 × 13
   respID `1_1` `1_2` `1_3` `2_1` `2_2` `2_3` `3_1` `3_2` `3_3` `4_1` `4_2`
    <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
 1      1     5     4     3     2     3     6     4     5     1     3     2
 2      2     6     1     5     1     6     2     5     4     3     2     3
 3      3     4     5     1     3     2     4     6     1     5     1     6
 4      4     5     4     3     2     3     6     4     5     1     3     2
 5      5     6     1     5     1     6     2     5     4     3     2     3
 6      6     4     5     1     3     2     4     6     1     5     1     6
 7      7     5     4     3     2     3     6     4     5     1     3     2
 8      8     6     1     5     1     6     2     5     4     3     2     3
 9      9     4     5     1     3     2     4     6     1     5     1     6
10     10     5     4     3     2     3     6     4     5     1     3     2
# ℹ 1 more variable: `4_3` <int>

上の出力は、行が調査対象者、行が試行x選択肢、値がプロファイル番号である。

左上から右に向かってみていこう。調査対象者1の試行1はプロファイル{5,4,3}, 試行2は{2,3,6}, 試行3は{4,5,1}, 試行4は{3,2,4}、調査対象者2の試行1は{6,1,5}, 試行2は{1,6,2}。ここまでで、ありうる6個のプロファイルすべてが、各選択肢において1回ずつ、計3回ずつ使われている。で、調査対象者2の試行3以降では、先頭に戻り、{5,4,3}, {2,3,6}, {4,5,1}, … と繰り返されている。

この生成方法においては、プロファイル数と試行数の最大公約数を試行数で割った値の人数(上の例では3人)をまとめてみたとき、ある選択肢番号においてすべてのプロファイルが同じ回数だけ登場する。つまり、3人ごとのブロックでみれば、水準の均等性と属性の直交性が達成される。しかし個人レベルでは達成されない。

この生成方法は、いっけん調査対象者によって実験計画が異なるようにみえて、実はそうではないという点に注意されたい。たとえば調査対象者1, 4, 7, 10は同じ実験計画である。

• ケース2, ありうるプロファイル数が試行数と同じ場合。試行数を6に増やしてみる。

set.seed(123)
demo_full_2 <- cbc_design(
  profiles = profiles_2x3,
  n_resp   = 10,      # 調査対象者数
  n_alts   = 3,       # 試行あたり選択肢数。ただし「どれも選ばない」は除く
  n_q      = 6,       # 調査対象者あたり試行数。プロファイル数と一致
  no_choice = FALSE,  # 「どれも選ばない」を含めない
  method   = 'full'   # 実験計画の生成方法
)

生成された実験計画をみてみよう。

demo_full_2 %>% 
  dplyr::select(respID, qID, altID, profileID) %>%
  pivot_wider(names_from = c(qID, altID), values_from = profileID) %>%
  print(.)

# A tibble: 10 × 19
   respID `1_1` `1_2` `1_3` `2_1` `2_2` `2_3` `3_1` `3_2` `3_3` `4_1` `4_2`
    <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
 1      1     5     4     3     2     3     6     4     5     1     3     2
 2      2     5     4     3     2     3     6     4     5     1     3     2
 3      3     5     4     3     2     3     6     4     5     1     3     2
 4      4     5     4     3     2     3     6     4     5     1     3     2
 5      5     5     4     3     2     3     6     4     5     1     3     2
 6      6     5     4     3     2     3     6     4     5     1     3     2
 7      7     5     4     3     2     3     6     4     5     1     3     2
 8      8     5     4     3     2     3     6     4     5     1     3     2
 9      9     5     4     3     2     3     6     4     5     1     3     2
10     10     5     4     3     2     3     6     4     5     1     3     2
# ℹ 7 more variables: `4_3` <int>, `5_1` <int>, `5_2` <int>, `5_3` <int>,
#   `6_1` <int>, `6_2` <int>, `6_3` <int>

どの調査対象者も全く同じ実験計画となる。 ある選択肢番号においてすべてのプロファイルが1回ずつ登場する。つまり、すべてのプロファイルが(選択肢数)回提示される。従って、元のプロファイルが属性の水準のすべての組み合わせである限り、水準の均等性と属性の直交性が個人レベルで達成される。文字通りの完全要因実施計画である。

• ケース3, ありうるプロファイル数が試行数より少ない場合。試行数を8に増やしてみる。

set.seed(123)
demo_full_3 <- cbc_design(
  profiles = profiles_2x3,
  n_resp   = 10,      # 調査対象者数
  n_alts   = 3,       # 試行あたり選択肢数。ただし「どれも選ばない」は除く
  n_q      = 8,       # 調査対象者あたり試行数。プロファイル数より多い
  no_choice = FALSE,  # 「どれも選ばない」を含めない
  method   = 'full'   # 実験計画の生成方法
)

出力された実験計画を見ると…

demo_full_3 %>% 
  dplyr::select(respID, qID, altID, profileID) %>%
  pivot_wider(names_from = c(qID, altID), values_from = profileID) %>%
  print(.)

# A tibble: 10 × 25
   respID `1_1` `1_2` `1_3` `2_1` `2_2` `2_3` `3_1` `3_2` `3_3` `4_1` `4_2`
    <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
 1      1     5     4     3     2     3     6     4     5     1     3     2
 2      2     4     5     1     3     2     4     6     1     5     1     6
 3      3     6     1     5     1     6     2     5     4     3     2     3
 4      4     5     4     3     2     3     6     4     5     1     3     2
 5      5     4     5     1     3     2     4     6     1     5     1     6
 6      6     6     1     5     1     6     2     5     4     3     2     3
 7      7     5     4     3     2     3     6     4     5     1     3     2
 8      8     4     5     1     3     2     4     6     1     5     1     6
 9      9    NA    NA    NA    NA    NA    NA    NA    NA    NA    NA    NA
10     10    NA    NA    NA    NA    NA    NA    NA    NA    NA    NA    NA
# ℹ 13 more variables: `4_3` <int>, `5_1` <int>, `5_2` <int>, `5_3` <int>,
#   `6_1` <int>, `6_2` <int>, `6_3` <int>, `7_1` <int>, `7_2` <int>,
#   `7_3` <int>, `8_1` <int>, `8_2` <int>, `8_3` <int>

なんと、対象者8以降で欠損が生じている。なぜか？　プロファイル数が6なので、Step 4が終わった段階で、(実際の試行数がどうであれ)試行6までの実験計画しか作られていないからである。

このようにcbc_design()は、生成方法がfullで、ありうるプロファイル数が試行数より小さいとき、欠損のある実験計画をしれっと返す。プロファイル数が試行数より少ないというのは実務的にはちょっと考えにくいケースではあるけれど、本来はエラーを発生させるべきだと思う。

6.3 orthogonal

orthogonal design(直交計画)の略。

説明の都合上、ここでは3属性、3x3x3水準とする。ありうるプロファイル数は3x3x3=27である。調査対象者数を10, 試行数を4, 選択肢数を3, 「どれも選ばない」提示なしとする。生成すべき実験計画は10x4x3=120行である。

profiles_3x3x3 <- cbc_profiles(
  A = c("A1", "A2", "A3"), 
  B = c("B1", "B2", "B3"), 
  C = c("C1", "C2", "C3")
)
set.seed(123)
demo_orthogonal <- cbc_design(
  profiles = profiles_3x3x3,   
  n_resp   = 10,    # 調査対象者数
  n_alts   = 3,    # 試行あたり選択肢数。ただし「どれも選ばない」は除く
  n_q      = 4,    # 調査対象者あたり試行数
  no_choice = FALSE,  # 「どれも選ばない」を含めない
  method   = 'orthogonal'  # 実験計画の生成方法
)

Orthogonal array found; using 9 out of 27 profiles for design

なにやらメッセージが出ていますね。

ソースコードを調べると( cbcTools:::make_design_orthogonal() )、実験計画は次の手順で生成されているようだ。

1. DoE.baseパッケージのoa.design()関数をコールする。上の場合、次のようなコードになる。

set.seed(123)
oa <- DoE.base::oa.design(
  factor.names = list(
    A = c("A1", "A2", "A3"), 
    B = c("B1", "B2", "B3"), 
    C = c("C1", "C2", "C3")
  )
)
oa <- as.data.frame(oa)

出力をみてみよう。

print(oa)

   A  B  C
1 A1 B3 C2
2 A2 B3 C1
3 A3 B3 C3
4 A1 B2 C3
5 A3 B2 C1
6 A2 B2 C2
7 A3 B1 C2
8 A1 B1 C1
9 A2 B1 C3

ありうる27個のプロファイルから、9個のプロファイルが取り出されている。

oa.design()関数とは直交配列を生成する関数である。直交配列とは、どの列をとっても値が同じ行数だけ出現し、どの2列をとっても値の組み合わせが同じ行数だけ出現する、という性質を持つ配列のことである。実験計画法の基礎的な概念であり、実験計画法の教科書にはいろんな直交配列が掲載されている。上の出力は、実験計画法の世界で\(L_9(3^4)\)という通称で呼ばれている直交配列から、3列を取り出してきたものになっている。

直交配列の列を属性、行をプロファイルとみると、水準の均等性と属性の直交性が達成されている。しかも、行数は元のプロファイル数より少ない(27個あったのが9個に減っている)。このような都合のよい直交配列がみつかったら、それを実験計画にしちゃえば効率がよい。

問題は、都合の良い直交配列はそうそう見つからないという点である。2属性、3x4水準について試してみよう。

oa <- DoE.base::oa.design(
  factor.names = list(
    A = c("A1", "A2", "A3"), 
    B = c("B1", "B2", "B3", "B4")
  )
)

creating full factorial with 12 runs ...

oa <- as.data.frame(oa)

なにやらメッセージが出ている。出力をみると…

print(oa)

    A  B
1  A3 B2
2  A3 B3
3  A1 B4
4  A2 B2
5  A3 B1
6  A2 B3
7  A1 B1
8  A1 B2
9  A3 B4
10 A2 B4
11 A1 B3
12 A2 B1

12行の配列が作られてしまった。つまり、単にすべての水準の組み合わせが出力されている。 2属性3x4水準の場合、行数が12行より小さくなるような都合のよい直交配列は存在しないのである。

良い直交配列が見つからない場合、oa.design()関数は単にすべての水準の組み合わせを返す。従ってこの場合は、cbc_design()関数で生成方法としてorthogonalを指定しても、fullを指定したのと同じことになる。

ここから先はfullのStep 2以降と同じである。おさらいすると…

2. 1.を選択肢数だけ繰り返し、出来上がった(選択肢数)個の行列を縦に積み上げ、1.でつけた行番号でソートする。上の例では9x3 = 27行。
3. こうしてできた行列をある一人の調査対象者の実験計画とみなして、上から順に、試行1の選択肢1, 2, …, 試行2の選択肢1, 2, …とする。最後の行は試行9となる。
4. もし、試行のなかでプロファイルが重複している試行、ならびに、全く同一のプロファイルを提示する複数の試行が存在したら、この行列を丸ごと捨てて、1.からやり直す。
5. この行列を調査対象者数だけ複製し、縦に積み上げる。上の例では270行。
6. この行列の上から、(調査対象者数x試行数x選択肢数)行を取り出す。上の例では10x3x4 = 120行。
7. こうしてできた行列を、(調査対象者数)人ぶんの実験計画とみなし、試行番号を振り直す。上から順に、調査対象者1の試行1の選択肢1, 2, …, 試行2の…, 調査対象者2の試行1の, … となる。

この生成方法の挙動について考えよう。4つのケースに分けられる。

• ケース0. 良い直交配列が得られない場合。たいていはこのケースとなる。生成方法としてfullを指定したのと同じことになる。

• ケース1. 運良く良い直交配列が得られ、その直交配列の行数が試行数より大きい場合。

demo_orthogonal %>% 
  dplyr::select(respID, qID, altID, profileID) %>%
  pivot_wider(names_from = c(qID, altID), values_from = profileID) %>%
  print(.)

# A tibble: 10 × 13
   respID `1_1` `1_2` `1_3` `2_1` `2_2` `2_3` `3_1` `3_2` `3_3` `4_1` `4_2`
    <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
 1      1    12    20    14    22    12    16    14     1    20     1    27
 2      2    16     6    22    27     8     1     8    14     6     6    16
 3      3    20    22     8    12    20    14    22    12    16    14     1
 4      4     1    27    12    16     6    22    27     8     1     8    14
 5      5     6    16    27    20    22     8    12    20    14    22    12
 6      6    14     1    20     1    27    12    16     6    22    27     8
 7      7     8    14     6     6    16    27    20    22     8    12    20
 8      8    22    12    16    14     1    20     1    27    12    16     6
 9      9    27     8     1     8    14     6     6    16    27    20    22
10     10    12    20    14    22    12    16    14     1    20     1    27
# ℹ 1 more variable: `4_3` <int>

この場合、直交配列の行数と試行数の最大公約数を試行数で割った値の人数(上の例では9人)を1ブロックとしてみたとき、ブロック内で水準の均等性と属性の直交性が達成される。しかし個人レベルでは、水準の均等性と属性の直交性は達成されない。

fullと同様、いっけん個人間で実験計画が異なるように見えて実はそうではないという点に注意されたい。各ブロックに対して同じ実験計画が使い回しされる。上の例では、調査対象者1と10は同じ実験計画となる。

• ケース2. 運良く良い直交配列が得られ、その行数がたまたま試行数と同じ場合。どの調査対象者も同じ実験計画となり、水準の均等性と属性の直交性が個人レベルで達成される。

• ケース3. 運良く良い直交配列が得られ、その行数が試行数より小さい場合。

set.seed(123)
demo_orthogonal_3 <- cbc_design(
  profiles = profiles_3x3x3,   
  n_resp   = 10,    # 調査対象者数
  n_alts   = 3,    # 試行あたり選択肢数。ただし「どれも選ばない」は除く
  n_q      = 10,    # 調査対象者あたり試行数
  no_choice = FALSE,  # 「どれも選ばない」を含めない
  method   = 'orthogonal'  # 実験計画の生成方法
)

Orthogonal array found; using 9 out of 27 profiles for design

demo_orthogonal_3 %>% 
  dplyr::select(respID, qID, altID, profileID) %>%
  pivot_wider(names_from = c(qID, altID), values_from = profileID) %>%
  print(.)

# A tibble: 10 × 31
   respID `1_1` `1_2` `1_3` `2_1` `2_2` `2_3` `3_1` `3_2` `3_3` `4_1` `4_2`
    <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
 1      1    12    20    14    22    12    16    14     1    20     1    27
 2      2    22    12    16    14     1    20     1    27    12    16     6
 3      3    14     1    20     1    27    12    16     6    22    27     8
 4      4     1    27    12    16     6    22    27     8     1     8    14
 5      5    16     6    22    27     8     1     8    14     6     6    16
 6      6    27     8     1     8    14     6     6    16    27    20    22
 7      7     8    14     6     6    16    27    20    22     8    12    20
 8      8     6    16    27    20    22     8    12    20    14    22    12
 9      9    20    22     8    12    20    14    22    12    16    14     1
10     10    NA    NA    NA    NA    NA    NA    NA    NA    NA    NA    NA
# ℹ 19 more variables: `4_3` <int>, `5_1` <int>, `5_2` <int>, `5_3` <int>,
#   `6_1` <int>, `6_2` <int>, `6_3` <int>, `7_1` <int>, `7_2` <int>,
#   `7_3` <int>, `8_1` <int>, `8_2` <int>, `8_3` <int>, `9_1` <int>,
#   `9_2` <int>, `9_3` <int>, `10_1` <int>, `10_2` <int>, `10_3` <int>

調査対象者10が欠損になっている。fullの場合と同じく、欠損のある実験計画をしれっと返してくる。

fullの場合、ありうるプロファイル数はふつう多いので、ケース3は生じにくい。ところがorthogonalの場合、運よく都合のいい直交配列がみつかるとプロファイル数が絞られてしまうので、ケース3がfullの場合より生じやすくなる。やっぱり、本来はエラーを発生させるべきだと思う。

6.4 dopt

D-optimal design(D-最適計画)の略。

説明の都合上、3属性、3x3x2水準とする。ありうるプロファイルの数は3x3x2=18個。調査対象者数を10, 試行数を7, 選択肢数を3, 「どれも選ばない」提示なしとする。生成すべき実験計画は10x7x3=210行である。

set.seed(123)
profiles_3x3x2 <- cbc_profiles(
  A = c("A1", "A2", "A3"), 
  B = c("B1", "B2", "B3"), 
  C = c("C1", "C2")
)
demo_dopt <- cbc_design(
  profiles = profiles_3x3x2,  
  n_resp   = 10,      # 調査対象者数
  n_alts   = 3,       # 試行あたり選択肢数。ただし「どれも選ばない」は除く
  n_q      = 7,       # 調査対象者あたり試行数
  no_choice = FALSE,  # 「どれも選ばない」を含めない
  method   = 'dopt'   # 実験計画の生成方法, 
)

D-optimal design found with D-efficiency of 0.527

ソースコードを調べると( cbcTools:::make_design_dopt() )、実験計画は次の手順で生成されているようだ。

1. AlgDesignパッケージのoptFederov()関数をコールする。上の場合、次のようなコードになる。

set.seed(123)
des <- AlgDesign::optFederov(
  frml = ~.,
  data = profiles_3x3x2[, -1],  # 1列目はプロファイル番号なので消している
  nTrials = 7  # 試行数
)
print(des)

$D
[1] 0.2426259

$A
[1] 6.611111

$Ge
[1] 0.527

$Dea
[1] 0.408

$design
    A  B  C
1  A1 B1 C1
5  A2 B2 C1
6  A3 B2 C1
7  A1 B3 C1
11 A2 B1 C2
13 A1 B2 C2
18 A3 B3 C2

$rows
[1]  1  5  6  7 11 13 18

このコードによって、ありうるプロファイル(ここでは18個)から試行数ぶんのプロファイル(7個)が取り出される。どういう7個かというと「線形回帰モデルの計画行列のD-最適性が最大に近い7個」である。

実際には、プロファイルの数が多いとき、すべての取り出し方について検討するのはむずかしい。そのためoptFederov()関数は、Federov交換アルゴリズムという方法を用い、現実的な時間のなかで、できる限りD-最適性が高くなる取り出し方を探す。

上の例では、27個のプロファイルのうち1,5,6,7,11,13,18番目が取り出された。 なお、cbc_design()は”D-optimal design found with D-efficiency of 0.527”というメッセージを 表示した。0.527とはeval.design()の返し値のうちGeに格納されている値で、 なんなのかいまいちよく理解できていないんだけど、 D-最適性を別のやり方で表現しているのだと思う。

ここから先はfullのStep 2以降と同じである。おさらいすると…

2. 1.を選択肢数だけ繰り返し、出来上がった(選択肢数)個の行列を縦に積み上げ、1.でつけた行番号でソートする。上の例では4x3 = 12行。
3. こうしてできた行列をある一人の調査対象者者の実験計画とみなして、上から順に、試行1の選択肢1, 2, …, 試行2の選択肢1, 2, …とする。最後の行は試行4、つまり、実際の試行数となる。
4. もし、試行のなかでプロファイルが重複している試行、ならびに、全く同一のプロファイルを提示する複数の試行が存在したら、この行列を丸ごと捨てて、1.からやり直す。
5. この行列を調査対象者数だけ複製し、縦に積み上げる。上の例では120行。
6. この行列の上から、(調査対象者数x試行数x選択肢数)行を取り出す。上の例では10x3x4 = 120行、つまり、すべてを取り出すことになる。
7. こうしてできた行列を、(調査対象者数)人ぶんの実験計画とみなす。

出力をみてみよう。

demo_dopt %>% 
  dplyr::select(respID, qID, altID, profileID) %>%
  pivot_wider(names_from = c(qID, altID), values_from = profileID) %>%
  print(.)

# A tibble: 10 × 22
   respID `1_1` `1_2` `1_3` `2_1` `2_2` `2_3` `3_1` `3_2` `3_3` `4_1` `4_2`
    <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
 1      1    18     6     5    11     5     6     7    18    13     6    11
 2      2    18     6     5    11     5     6     7    18    13     6    11
 3      3    18     6     5    11     5     6     7    18    13     6    11
 4      4    18     6     5    11     5     6     7    18    13     6    11
 5      5    18     6     5    11     5     6     7    18    13     6    11
 6      6    18     6     5    11     5     6     7    18    13     6    11
 7      7    18     6     5    11     5     6     7    18    13     6    11
 8      8    18     6     5    11     5     6     7    18    13     6    11
 9      9    18     6     5    11     5     6     7    18    13     6    11
10     10    18     6     5    11     5     6     7    18    13     6    11
# ℹ 10 more variables: `4_3` <int>, `5_1` <int>, `5_2` <int>, `5_3` <int>,
#   `6_1` <int>, `6_2` <int>, `6_3` <int>, `7_1` <int>, `7_2` <int>,
#   `7_3` <int>

実験計画はすべての対象者で同一となる。水準の均等性と属性の直交性は保証されないが、D-最適性を(ほぼ)最大化する実験計画だから、水準の均等性も属性の直交性も、それなりに達成されている… と期待できる。

確かめよう。 調査対象者1における各水準の出現頻度をみると…

demo_dopt %>%
  dplyr::filter(respID == 1) %>%
  pivot_longer(cols = c(A,B), names_to = "sAtt", values_to = "sValue") %>%
  group_by(sAtt, sValue) %>%
  summarize(nFreq = n()) %>%
  ungroup() %>%
  print(.)

# A tibble: 6 × 3
  sAtt  sValue nFreq
  <chr> <fct>  <int>
1 A     A1         9
2 A     A2         6
3 A     A3         6
4 B     B1         6
5 B     B2         9
6 B     B3         6

属性Aの各水準の出現頻度は9,9,6, 属性Bの各水準の出現頻度は6,9,6となっている(生成手順の性質上、かならず選択肢数の倍数になる)。水準の均等性は達成されていないが、それなりに頑張って揃えていることがわかる。

調査対象者1について、2属性のクロス表をみると…

table(demo_dopt[demo_dopt$respID == 1,]$A, demo_dopt[demo_dopt$respID == 1,]$B)

    
     B1 B2 B3
  A1  3  3  3
  A2  3  3  0
  A3  0  3  3

各組み合わせの頻度は3ないし0となっている(生成手順の性質上、かならず選択肢数の倍数になる)。属性の直交性は達成されていないけれど、 それに近い状態にはなっている。

ところで、D-最適性を最大化する実験計画は、実は一意に決まらない。

上の事例に戻って調べてみよう。18個のプロファイルから7個を取り出す取り出し方は31824通りしかないので、Federov交換アルゴリズムを使わなくても、頑張ればすべて調べることができるはずだ。

31824通りの実験計画のすべてについてD-最適性を求めてみた。そもそもD-最適性を求められない計画も多数あるので(使われていない水準がある計画とか)、 下のコードでは、エラーになったらNAとなるように工夫している。

mnCombn <- combn(18,7)
agOptimality <- sapply(
  seq_len(ncol(mnCombn)), 
  function(nID){
    dfChoosed <- as.data.frame(profiles_3x3x2[mnCombn[,nID], -1])
    out <- try(eval.design(~., design = dfChoosed)$determinant, silent = TRUE)
    if (class(out) == "try-error") out <- NA
    return(out)
  }
)

D-最適性が得られた実験計画の数と、得られたD-最適性の分布、ならびに、最大値を調べよう。

length(agOptimality[!is.na(agOptimality)])

[1] 25399

hist(agOptimality)

max(agOptimality, na.rm = TRUE)

[1] 0.2426259

D-最適性を求めることができた実験計画は25399個。ヒストグラムからは、一握りの「D-最適性が高い実験計画」があることがわかる。D-最適性の最大値は0.2426259。では、D-最適性がもっとも高い実験計画は何個目か？

gMaxOpt <- max(agOptimality, na.rm=TRUE)
abMax <- (!is.na(agOptimality) & gMaxOpt - agOptimality == 0)
anMaxPlan <- seq_along(abMax)[abMax]
print(anMaxPlan)

[1] 16435 20933 22506

なんと、3つあるぞ。どんな実験計画だろうか？

mnCombn[, anMaxPlan]

     [,1] [,2] [,3]
[1,]    2    3    3
[2,]    4    4    5
[3,]    6    5    6
[4,]    9    9    7
[5,]   12   11   11
[6,]   14   15   13
[7,]   16   16   18

たとえば、2,4,6,9,12,14,16番目のプロファイルを取り出す実験計画がそれである。あれれ？ さっきoptFederov()関数が返してきた計画が含まれていないぞ？

実は、実験計画のうちD-最適性が最大に近い計画はほかにもある。

abNearMax <- (!is.na(agOptimality) & gMaxOpt - agOptimality < 0.0000001)
anNearMaxPlan <- seq_along(abNearMax)[abNearMax]
print(anNearMaxPlan)

  [1]  2212  2924  3215  3338  3419  3422  5119  5709  5829  5834  5918  6324
 [13]  7920  8343  8955  8967  9493  9507  9613  9711 10041 10242 10467 10468
 [25] 10474 10484 10485 10496 10505 10507 10516 10735 11046 11133 11135 11137
 [37] 11149 11154 11160 11167 11169 11180 12985 12987 13105 13191 13702 14195
 [49] 15908 16197 16317 16351 16435 16733 16975 17157 17158 17161 17176 17177
 [61] 17182 17231 17234 17237 17515 18020 18049 18726 18841 18897 18901 18902
 [73] 18912 18918 18924 18966 18967 18973 20709 20849 20913 20933 21322 21652
 [85] 21968 22023 22024 22026 22055 22057 22059 22090 22094 22097 22506 22956
 [97] 23025 23096 23102 23103 23127 23131 23140 23162 23163 23166 23731 23748

いっぽう、optFederov()関数が返した計画は…

anTarget <- c(1,5,6,7,11,13,18)
which(apply(mnCombn, 2, function(x) all.equal(x, anTarget)) == "TRUE")

[1] 9493

31824通りの計画のなかのNo.9493であった。この計画のD-最適性は、D-最適性が最大である3つの計画のD-最適性よりほんのわずかに低いのだが、これは実験計画の性質の違いというより、ただの計算誤差かもしれない。

このように、optFederov()関数はD-最適性が最大に近そうな計画を選んで返してくれるけれど、(ほぼ)同じD-最適性を持つ計画がほかにたくさんあるかもしれない。

6.5 CEA

Coordinate Exchange Algorithm(座標交換アルゴリズム)の略。次項で説明するModfedとよく似ている。まとめてベイジアン最適計画と呼ぶことができる。

試してみよう。引き続き、3属性、3x3x2水準とする。プロファイル数は18。調査対象者数10, 試行数7, 選択肢数3, 「どれも選ばない」提示なしとする。生成すべき実験計画は10x7x3=210行である。

この方法は、実験計画をDB-最適性に基づいて生成するので、パラメータの事前分布を与える必要がある。priors引数で、各パラメータの事前分布の平均を指定する。 下の例では、どの水準もパラメータはたぶん0くらいだろう、という信念を与えている (平均はすべて0, 分散はすべて1, 共分散はすべて0の多変量正規分布を与えたことになる)。

set.seed(123)
demo_CEA <- cbc_design(
  profiles = profiles_3x3x2,  
  n_resp   = 10,      # 調査対象者数
  n_alts   = 3,       # 試行あたり選択肢数。ただし「どれも選ばない」は除く
  n_q      = 7,       # 調査対象者あたり試行数
  no_choice = FALSE,  # 「どれも選ばない」を含めない
  method   = 'CEA',   # 実験計画の生成方法
  priors   = list(A = c(0,0), B = c(0, 0), C = 0) # 事前分布の平均
)

Bayesian D-efficient design found with DB-error of 1.19942

生成されたデザインのDB-誤差が表示されている。1.19942だそうです。

ソースコードを調べると( cbcTools:::make_design_bayesian() )、実験計画は次の手順で生成されているようだ。

1. idefixパッケージのCEA()関数をコールする。上の例の場合、こういうコードとなる。

set.seed(123)
# 事前分布をつくる
dfDraw <- MASS::mvrnorm(n = 50, mu = c(0,0,0,0,0), Sigma = diag(5))
D <- idefix::CEA(
  lvls   = c(3, 3, 2),       # 属性の水準数
  coding = c("D", "D", "D"), # いずれの属性も離散的属性
  par.draws = dfDraw,        # 事前分布
  n.alts = 3,                # 選択肢数
  n.sets = 7,                # 試行数
  no.choice = FALSE,         # 「どれも選ばない」はなし
  n.start = 5, 
  parallel = FALSE
)

出力をみてみよう。

print(D)

$design
          Var12 Var13 Var22 Var23 Var32
set1.alt1     0     0     0     1     1
set1.alt2     1     0     1     0     1
set1.alt3     0     1     0     0     0
set2.alt1     0     0     1     0     1
set2.alt2     1     0     0     0     0
set2.alt3     0     1     0     1     0
set3.alt1     0     1     0     0     1
set3.alt2     0     0     1     0     0
set3.alt3     1     0     0     1     0
set4.alt1     0     0     0     0     0
set4.alt2     0     1     1     0     1
set4.alt3     1     0     0     1     1
set5.alt1     1     0     1     0     0
set5.alt2     0     1     0     1     1
set5.alt3     0     0     0     0     1
set6.alt1     0     0     1     0     0
set6.alt2     0     0     0     1     0
set6.alt3     1     0     0     0     1
set7.alt1     0     1     1     0     0
set7.alt2     0     0     0     0     1
set7.alt3     1     0     1     0     1

$error
[1] 1.199418

$inf.error
[1] 0

$probs
      Pr(alt1)  Pr(alt2)  Pr(alt3)
set1 0.3829093 0.2792705 0.3378202
set2 0.3200756 0.3083087 0.3716157
set3 0.3511385 0.2653445 0.3835169
set4 0.3032373 0.3119863 0.3847763
set5 0.3244054 0.3764404 0.2991541
set6 0.2738039 0.3680414 0.3581548
set7 0.3298759 0.3849791 0.2851449

CEA()は、18個のプロファイルから7試行ぶんの実験計画を作り出す。その際の基準は、指定された事前分布のもとで「多項ロジットモデルにおけるDB-誤差が最小となる実験計画を選ぶ」である。

2. この行列を調査対象者数だけ複製し、縦に積み上げる。上の例では210行。
3. この行列の上から、(調査対象者数x試行数x選択肢数)行を取り出す。上の例では10x7x3 = 210行、つまり、すべてを取り出すことになる。

では、出力をみてみよう。

demo_CEA %>% 
  dplyr::select(respID, qID, altID, profileID) %>%
  pivot_wider(names_from = c(qID, altID), values_from = profileID) %>%
  print(.)

# A tibble: 10 × 22
   respID `1_1` `1_2` `1_3` `2_1` `2_2` `2_3` `3_1` `3_2` `3_3` `4_1` `4_2`
    <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
 1      1    16    14     3    13     2     9    12     4     8     1    15
 2      2    16    14     3    13     2     9    12     4     8     1    15
 3      3    16    14     3    13     2     9    12     4     8     1    15
 4      4    16    14     3    13     2     9    12     4     8     1    15
 5      5    16    14     3    13     2     9    12     4     8     1    15
 6      6    16    14     3    13     2     9    12     4     8     1    15
 7      7    16    14     3    13     2     9    12     4     8     1    15
 8      8    16    14     3    13     2     9    12     4     8     1    15
 9      9    16    14     3    13     2     9    12     4     8     1    15
10     10    16    14     3    13     2     9    12     4     8     1    15
# ℹ 10 more variables: `4_3` <int>, `5_1` <int>, `5_2` <int>, `5_3` <int>,
#   `6_1` <int>, `6_2` <int>, `6_3` <int>, `7_1` <int>, `7_2` <int>,
#   `7_3` <int>

実験計画はすべての対象者で同一となる。水準の均等性と属性の直交性は保証されないが、DB-最適性を(ほぼ)最大化する実験計画だから、水準の均等性も属性の直交性も、それなりに得られているいると期待できる。さらにいえば、この手法はdoptとは異なり試行ごとの最適性を考慮しているので、水準の最小重複もある程度得られていると期待できる。

調べてみよう。まず水準の均等性。

demo_CEA %>%
  dplyr::filter(respID == 1) %>%
  pivot_longer(cols = c(A,B), names_to = "sAtt", values_to = "sValue") %>%
  group_by(sAtt, sValue) %>%
  summarize(nFreq = n()) %>%
  ungroup() %>%
  print(.)

# A tibble: 6 × 3
  sAtt  sValue nFreq
  <chr> <fct>  <int>
1 A     A1         8
2 A     A2         7
3 A     A3         6
4 B     B1         7
5 B     B2         8
6 B     B3         6

6,7,8のいずれかになっている(doptとは異なり、試行ごとの計画行列を最適化しようとしているので、選択肢数の倍数にはならない)。頑張ってますね。

属性の直交性。

table(demo_CEA[demo_dopt$respID == 1,]$A, demo_CEA[demo_dopt$respID == 1,]$B)

    
     B1 B2 B3
  A1  3  3  2
  A2  2  3  2
  A3  2  2  2

2,3のいずれかになっている。おお、いい感じだ。

水準の最小重複。

demo_CEA %>%
  dplyr::filter(respID == 1) %>%
  dplyr::select(qID, A, B) %>%
  pivot_longer(cols = c(A, B), names_to = "attribute", values_to = "level") %>%
  group_by(qID, attribute) %>%
  summarize(n_usedlevel = length(unique(level))) %>%
  ungroup() %>%
  group_by(attribute, n_usedlevel) %>%
  summarize(freq = n()) %>%
  ungroup() %>%
  pivot_wider(names_from = c(attribute, n_usedlevel), values_from = freq) %>%
  print(.)

# A tibble: 1 × 4
    A_2   A_3   B_2   B_3
  <int> <int> <int> <int>
1     1     6     1     6

ちょっとわかりにくい集計だが、Aについて水準の重複のない試行が6試行、Bについて水準の重複のない試行が6試行。すごい、頑張ったね。

6.6 Modfed

Modified Fedorov algorithm(修正Fedorovアルゴリズム)の略。CEAとよく似ている。

CEAと全く同じ設定で試してみる。

set.seed(123)
demo_Modfed <- cbc_design(
  profiles = profiles_3x3x2,  
  n_resp   = 10,         # 調査対象者数
  n_alts   = 3,          # 試行あたり選択肢数。ただし「どれも選ばない」は除く
  n_q      = 7,          # 調査対象者あたり試行数
  no_choice = FALSE,     # 「どれも選ばない」を含めない
  method   = 'Modfed',   # 実験計画の生成方法
  priors   = list(A = c(0,0), B = c(0, 0), C = 0) # 事前の確率分布の平均
)

Bayesian D-efficient design found with DB-error of 1.2037

生成された実験計画のDB-誤差は1.2037だそうです。CEAより少し大きい。

ソースコードを調べると( cbcTools:::make_design_bayesian() )、実験計画は次の手順で生成されているようだ。

1. idefixパッケージのModfed()関数をコールする。上の例の場合、こういうコードとなる。

set.seed(123)
# 事前分布をつくる
dfDraw <- MASS::mvrnorm(n = 50, mu = c(0,0,0,0,0), Sigma = diag(5))
D <- idefix::Modfed(
  cand.set = idefix::Profiles(
    lvls   = c(3, 3, 2),       # 属性の水準数
    coding = c("D", "D", "D"), # いずれの属性も離散的属性
  ),
  par.draws = dfDraw, # 事前分布 
  n.alts = 3,         # 選択肢数
  n.sets = 7,         # 試行数
  no.choice = FALSE,  # 「どれも選ばない」はなし
  n.start = 5, 
  parallel = FALSE
)

出力をみてみよう。

print(D)

$design
          Var12 Var13 Var22 Var23 Var32
set1.alt1     0     0     0     0     1
set1.alt2     0     1     0     1     0
set1.alt3     1     0     1     0     0
set2.alt1     0     1     0     0     1
set2.alt2     0     1     1     0     0
set2.alt3     0     0     1     0     1
set3.alt1     0     1     1     0     1
set3.alt2     1     0     0     1     0
set3.alt3     0     0     0     0     0
set4.alt1     1     0     0     1     0
set4.alt2     1     0     0     0     1
set4.alt3     0     0     0     1     1
set5.alt1     0     0     0     1     0
set5.alt2     1     0     1     0     1
set5.alt3     0     1     0     0     0
set6.alt1     0     1     0     1     1
set6.alt2     1     0     0     0     0
set6.alt3     0     0     1     0     0
set7.alt1     0     0     0     0     0
set7.alt2     0     1     1     0     0
set7.alt3     1     0     0     1     1

$error
[1] 1.2037

$inf.error
[1] 0

$probs
      Pr(alt1)  Pr(alt2)  Pr(alt3)
set1 0.3310272 0.3800593 0.2889135
set2 0.3860014 0.3072201 0.3067785
set3 0.3385256 0.3799615 0.2815128
set4 0.3363640 0.3028935 0.3607424
set5 0.3731940 0.3061257 0.3206803
set6 0.4059506 0.3243004 0.2697490
set7 0.2941884 0.3030599 0.4027517

あとはCEAと同じ。おさらいすると、

2. この行列を調査対象者数だけ複製し、縦に積み上げる。上の例では210行。
3. この行列の上から、(調査対象者数x試行数x選択肢数)行を取り出す。上の例では10x7x3 = 210行、つまり、すべてを取り出すことになる。

出力をみてみよう。

demo_Modfed %>% 
  dplyr::select(respID, qID, altID, profileID) %>%
  pivot_wider(names_from = c(qID, altID), values_from = profileID) %>%
  print(.)

# A tibble: 10 × 22
   respID `1_1` `1_2` `1_3` `2_1` `2_2` `2_3` `3_1` `3_2` `3_3` `4_1` `4_2`
    <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
 1      1    10     9     5    12     6    13    15     8     1     8    11
 2      2    10     9     5    12     6    13    15     8     1     8    11
 3      3    10     9     5    12     6    13    15     8     1     8    11
 4      4    10     9     5    12     6    13    15     8     1     8    11
 5      5    10     9     5    12     6    13    15     8     1     8    11
 6      6    10     9     5    12     6    13    15     8     1     8    11
 7      7    10     9     5    12     6    13    15     8     1     8    11
 8      8    10     9     5    12     6    13    15     8     1     8    11
 9      9    10     9     5    12     6    13    15     8     1     8    11
10     10    10     9     5    12     6    13    15     8     1     8    11
# ℹ 10 more variables: `4_3` <int>, `5_1` <int>, `5_2` <int>, `5_3` <int>,
#   `6_1` <int>, `6_2` <int>, `6_3` <int>, `7_1` <int>, `7_2` <int>,
#   `7_3` <int>

生成される実験計画の性質はCEAと同じである。CEAとの違いは、DB-最適な実験計画をみつけるためのアルゴリズムである。idefixパッケージの作者らによれば、実験計画のサイズが小さいときにはModfedのほうがより効率的な実験計画をみつけてくれるが、実験計画のサイズが大きいときはCEAのほうが速い、とのことである。

7 まとめ

7.1 生成手法の比較

6つの手法により生成される実験計画の性質についてまとめておこう。

• random
  • 実験計画は対象者間で異なる
  • 集団レベルでの水準の均等性・属性の直交性は、対象者数x試行数が十分に大きければほぼ達成
  • 個人レベルでの水準の均等性・属性の直交性は、達成しようとしていない
  • 水準の最小重複は、達成しようとしていない
• full, orthogonal
  • 実験計画は対象者間で異なるが、何人かおきに同一
  • 集団レベルでの水準の均等性・属性の直交性は、ほぼ達成
  • 個人レベルでの水準の均等性・属性の直交性は、達成しようとしていない
  • 水準の最小重複は、達成しようとしていない
• dopt
  • 実験計画は対象者間で同一
  • 水準の均等性・属性の直交性は、できる限り達成
  • 水準の最小重複は、達成しようとしていない
• CEA, Modfed
  • 実験計画は対象者間で同一
  • 水準の均等性・属性の直交性は、できる限り達成
  • 水準の最小重複は、できる限り達成

7.2 さらなる話題

cbcToolsパッケージには、本稿で紹介しなかった機能もたくさんある。実験計画の生成については、

• プロファイルのprohibition
• alternative-specific 計画
• 計画のブロッキング

実験計画の評価については

• 架空回答データのお手軽生成
• 標本サイズとパラメータ推定精度の関係についてのシミュレーション

とはいえ、もう力尽きたので、本稿はこれでおしまいです。詳しくは cbcToolsパッケージの使用説明書 をご覧下さい。

7.3 よくわからないこと

ぐだぐだ偉そうに書いてきたけれど、実は以前から「よくわからんな…」と悩んでいることがあるので、ここに記録しておく。

選択型コンジョイント分析を行い、階層モデルによって個人レベル効用をベイズ推定する場面を考える。近年のWeb調査環境では、対象者によって試行の提示順序や選択肢の提示順をランダム化することは容易である。少なくとも、順序効果が特定の試行に強く影響することを避けるため、試行の順序は対象者間で変えた方がよいだろう。

では、対象者間で実験計画そのものも変えた方がよいだろうか？

たとえば、1人分の実験計画をD-最適計画により生成するとしますね。次のどちらがよいだろうか。

• すべての対象者で同一の実験計画を使う。対象者間で試行の提示順や選択肢の提示順を変える。
• D-最適性が同程度に高い実験計画を、たとえば5種類用意する。対象者を5群に分け、各群に異なる実験計画を用いる。さらに、対象者間で試行の提示順や選択肢の提示順を変える。

直感としては後者がよいのではないかと思うのだが、不勉強にして、いまだ明確な答えを得ていない。いずれシミュレーションで確かめてみたいと思っているんだけど…

7.4 現時点でのベスト・プラクティス？

最後に、選択型コンジョイント分析の実験計画生成について、現時点で私が考えている方針のようなものをメモしておく。ご批判を頂ければ幸いです。

Web調査、提示刺激の作成にはコストが掛からず、提示刺激を対象者間で変動させるのも容易、階層ベイズモデルで個人レベル効用を推定、交互作用効果は推定しない、という場面について考える。属性・水準、対象者数、試行数、選択肢数、「どれも選ばない」選択肢の有無、についてはすでに決定しているものとする。

• まずはDB-最適計画(CEA, Modfed)を試す。パラメータの値についてなんの事前知識もなかったら平均0とする。上手くいかなかったらD-最適計画(dopt)を試す。いずれの場合も、最適性が最良の計画をひとつ生成するのではなく、乱数のシードを変えながら生成を繰り返し、最適性が高い計画を多めに生成し、各計画について特徴を調べ、気に入った奴を(たとえば)5個選び、対象者をランダムに5群に割り当てる。
• どちらもうまくいかない場合は完全要因実施計画(full)を試す。本来の調査対象者数がどうであれ、(プロファイル数と試行数の最大公約数)/(試行数)人ぶんの実験計画を、乱数のシードを変えながらたくさん生成し、個人レベルでの実験計画の特徴について調べ、良い計画を(たとえば)5個選び、対象者をランダムに5群に割り当てる。
• 実験計画の特定の特徴を追求したい場合(たとえば水準の重複が許せない場合)、ランダム法(random)が選択肢となる。乱数のシードを変えながら実験計画を山のように生成し、求める特徴を持つ計画を見つけ出す。
• できれば作業時間を確保し、架空データによるシミュレーションで個人レベル・パラメータの復元性能を確認するとよい。その際はcbcToolsの機能に頼らず、自分で書いた方がよいだろう。データ収集後の分析の予行練習にもなる。
• ランダム法を除き、試行順序は個人間でランダマイズすること。もし必要なら選択肢の提示順のランダマイズも検討する。

以上！

8 更新履歴

• 2023/08/09: 初版を公開
• 2023/08/10: cbcTools 0.5.0のバグを報告したところ早速対応して下さった。バグについての記述を修正。
• 2023/08/11: 「生成方法の比較」を追加し、「現時点でのベスト・プラクティス？」を大幅改訂。ところで、cbcToolsの作者さんがこのページを読んでコメントを下さった。感動。